Dueling Network Architectures for Deep Reinforcement Learning
0. Abstract
▶ 최근 몇년 동안 RL에서 deep representation를 사용하는데 많은 성공을 거두었으나 이러한 application 중 상당수는 CNN, LSTM, auto-encoders와 같은 기존 architecture 사용
▶ 해당 논문에서는 Dueling network라는 두개의 개별 estimators인 RL을 위한 새로운 neural network architecture를 제시
→ 하나는 state-value function, 또 다른 하나는 state-dependent action-advantage function으로 사용
→ 이러한 factoring은 기본 RL algorithm에 변경 사항을 부과하지 않고 action 전반에 걸쳐 학습 일반화 가능
▶ Dueling network architecture은 더 좋은 policy evaluation으로 이어지고 기존의 performance를 능가
1. Introduction
▶ 최근 DL은 RL의 scalability와 performance에서 극적인 발전을 이루어 냈지만, 대부분의 접근 방식은 CNN, MLP, LSTM, auto-encoder와 같은 standard neural network를 사용
▶ 이러한 최근 발전의 초점은 향상된 control 및 RL algorithm을 설계하거나 기존의 RL neural network architecture를 RL method에 통합하는 것
▶ model-free RL에 더 적합한 neural network architecture에 초점을 맞추는 대안적이지만 보완적인 접근 방식을 취함
→ 이 접근 방식은 새로운 network가 RL에 대한 기존 및 미래 algorithm과 쉽게 결합 가능하다는 이점 보유
→ 즉, 해당 논문은 새로운 network를 발전시키지만 이미 공개된 algorithm을 사용
(1) Model architecture
▶ Dueling architecture network는 state-value & state-depentent action advantages를 명시적으로 분리▶ value & advantage function을 나타내는 두개의 stream로 구성되며 공통의 convolutional feature learning module를 공유
▶ 두개의 stream은 아래와 같이 state-action value function Q의 estimate를 생성하기 위해, special aggregating layer을 통해 결합
→ DQN에서 인기 있는 single Q network를 대체하고 두 개의 stream이 있는 single Q network로 이해해야 함
▶ Dueling network는 별도의 supervision 없이 state-value function과 advantage function에 대한 별도의 estimate를 자동으로 생성

(2) Advantage of model
▶ 직관적으로 Dueling architecture는 각 states에 대한 action의 효과를 학습하지 않고도 어떤 states가 가치있는지 학습 가능→ 해당 actions이 relevent way로 환경에 영향을 미치지 않는 states에서 특히 유용
▶ 아래 그림은 두 가지 다른 time-step에 대한 value & advantage saliency map을 제시
→ one time-step에서 value network stream이 도로, 특히 새 자동차가 등장하는 지평선, 점수에 주의를 기울임
→ advantage stream은 앞 차가 없을 경우 action 선택이 실질적으로 관련이 없기 때문에 visual input에 주의를 기울이지 않음
→ 그러나 two time-step에서 advantage stream은 바로 앞에 차가 있으므로 주의를 기울이고 action 선택을 적절하게 만듬

▶ 실험에서, 중복되거나 유사한 action이 학습 문제에 추가됨에 따라, Dueling architecture가 policy evaluation 중에 올바른 action을 더 빨리 식별할 수 있음을 보임
1.1 Related Work
-Baird's original advantage updating algorithm: shared Bellman residual update equation은 state-value function과 이에 연관된 advantage function으로 분해
→ advantage update는 continous time domain에서 Q-learning보다 빠르게 수렴
→ 이 후계자인 advantage learning algorithm은 single advantage function만을 표현
▶ Dueling architecture는 두 가지를 결합하여 state-action value Q(s,a)를 생성하는 single deep model로 value V(s)와 advantage A(s,a) functions를 모두 나타냄
▶ advantage updating과 다르게 representation과 algorithm은 consturuction에 의해 분리되어, 결과적으로 Dueling architecture는 무수히 많은 model-free RL algorithm과 결합하여 사용 가능
▶ policy gradient algorithm의 variance를 줄이기 위해 online으로 advantage values를 추정하는 시도 또한 존재
2. Background
(1) Precondition
▶ agent가 discrete time-step에 걸쳐 환경 ɛ와 interaction하는 sequential decision making setup
▶ 그런 다음 agent는 discrete set인 a_t A={1, ... , |A|}에서 action을 선택하고 game emulator에서 생성된 reward signal을 관찰
▶ agent는 아래의 expected discounted return을 최대화하려 동작
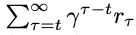
▶ stochastic policy π에 의해 행동하는 agent의 경우 state-action pair (s,a) 및 state s의 value은 다음과 같이 정의

▶ 앞의 state-action value function(Q-function)는 dynamic programming을 사용하여 재귀적으로 계산 가능

▶ optimal Q*(s,a)=max_π Q^π(s,a)를 정의
▶ deterministic policy에서 a=argmax_a' Q*(s,a')는 V*(s)=max_a Q*(s,a)를 따름
→ 이로부터 optimal Q-function은 Bellman equation을 만족

▶ value와 Q-function과 관련된 또 다른 중요한 요소인 advantage function을 다음과 같이 정의

▶ E_a~π(s) [A^π(s,a)] = 0 임을 명시

▶ value function V는 특정 state s에 있는 것이 얼마나 좋은지를 측정
▶ Q-function은 이 state에 있을 때 특정 action을 선택하는 value를 측정
▶ advantage function은 Q-function에서 state value를 빼서 각 action의 중요성에 대한 상대적인 measure를 얻음
2.1 DQN
▶ value function는 high dimensional object로 이를 approximate하기 위해 parameter θ와 함께 DQN; Q(s,a; θ) 사용
▶ network를 estimate하기 위해, iteration i에서 다음의 loss function sequence를 최적화
// θ-: parameters of fixed & seperate target network


▶ network Q(s,a;θ) parameter를 online으로 학습하기 위해 standard Q-learning을 사용할 수도 있지만 성능이 좋지 않음
▶ DQN의 핵심 혁신은 SGD로 online network Q(s,a;θ)를 update 하는동안 고정된 iteration 동안 target network Q(s',a';θ-) parameter를 고정시키는 것
→ 위 혁신은 algorithm의 안정성을 크게 향상시키며 특정 gradient update는 아래 참조

▶ 이러한 접근 방식은 state와 reward가 환경에 의해 생성된다는 점에서 model-free하고 이러한 state와 reward는 학습 중인 online policy와 다른 behavior policy(ex. epsilon greedy)로 얻어지기 때문에 off-policy
▶ 또다른 핵심요소로는 experience replay를 사용
▶ 학습 동안 agent는 많은 episode로부터 dataset D_t={e1, e2, ... , e_t} of experiences e_t={s_t, a_t, r_t, s_(t+1)) 축적
▶ Q-network를 훈련할 때, standard TD-learning에 의해 규정된 current experience만을 사용하는 대신 D에서 experience의 mini batch를 무작위로 균일하게 sampling하여 network를 훈련

▶ experience replay는 여러 update에서 experience smaples를 재사용하여 data efficiency를 높이고, replay buffer의 균일한 sampling이 update에 사용된 sample간의 correlation을 줄여 variance 감소
2.2 Double DQN
▶ Q-learning 및 DQN에서 max 연산자는 동일한 value를 사용하여 action을 선택하고 evaluate하여 overoptimistic value estimate로 이어질 수 있음
▶ 이러한 overestimate를 완화하기 위해 DDQN은 다음 target을 사용
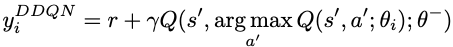
2.3 Prioritized Replay
▶ 학습 진도가 높을 것으로 예상되는 experience tuples의 재생 확률을 높이는 것으로 proxy of absolute TD-error로 측정
▶ 균일한 experience replay 보다 더 빠른 학습과 더 나은 final policy quality 결과를 보이며,
3. The Dueling Network Architecture
▶ new architecture의 핵심 통찰력은 많은 states에서 각 action 선택의 가치를 평가할 필요가 없다는 것
→ 어떤 states에서는 어떤 action을 취해야 하는지 아는 것이 가장 중요하지만 다른 많은 states에서는 action 선택이 무슨 일이 일어나는지에 영향을 미치지 않음
→ 그러나 bootstrapping based algorithm의 경우 states value의 estimation은 모든 states에서 중요
(1) Detail
▶ Dueling network의 lower layers는 DQN과 동일한 convolutional
→ 그러나 fully-connected layers의 single sequence로 convolutional layers를 따르는 것이 아닌, fully-connected layers의 두 개의 sequence(stream)을 사용
▶ stream은 value & advantage function에 대한 별도의 estimate를 제공할 수 있는 기능을 가지도록 구성
▶ 마지막으로 두 개의 stream이 결합되어 single output Q-function을 생성
→ network의 output은 각 action에 대한 각각의 Q-value
▶ Dueling network의 output은 Q-function이므로 DDQN, SQRSA와 같은 기존의 많은 algorithm으로 훈련 가능
→ 또한 더 나은 exploration policies, intrinsic motivation 등을 포함하여 이러한 algorithm의 개선 사항을 활용 가능
▶ Q-function을 출력하기 위해 fully-connected layer의 두 개의 stream을 결합하는 모듈은 신중한 설계가 필요
▶ 다음 표현에서 state-value V^π(s) = E_a~π(s) [Q^π(s,a)]는 E_a~π(s)[A^π(s,a)] = 0을 따름


▶ deterministic policy a* = argmax_a'∈A Q(s,a')에서 Q(s,a*) = V(s)를 따르고, 결국 A(s,a*) = 0
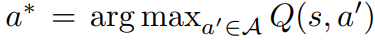
▶ fully-connected layer의 한 stream은 scalar V(s; θ, β)를 출력하고, 또 다른 stream은 |A|-dimensional vector A(s, a; θ, α) 출력
// θ: convolutional layer's parameter
// α, β: fully-connected layer의 두 개 stream의 parameter
(2) Aggregation
▶ advantage의 정의를 사용하여 다음과 같이 aggregating 모듈 설계 가능

▶ 위 표현은 모든 (s,a) instances에 적용되며, matrix form으로 표현하려면 scalar V (s θ, β)를 |A| times 복사
→ 그러나 Q(s, a; θ, α, β)는 true Q-function의 parameterized estimate일 뿐임
→ 추가로 V(s; θ, β)가 state-value function의 좋은 estimator이라고 결론짓거나 마찬가지로 A(s, a; θ, α)가 advantage function의 합리적인 estimate를 제공한다고 결론 짓는 것은 잘못된 것
▶ equation (7)은 주어진 Q가 V와 A를 고유하게 복구할 수 없다는 점에서 식별이 불가능
→ 이를 확인 하기 위해서는 V(s, θ, β)에 상수를 추가하고 A(s, a, θ, α)에서 동일한 상수를 빼면 상수가 상쇄되어 동일한 Q-value 생성
→ 이러한 식별 불가능함은 euqation (8)이 직접 사용될 때 열악한 실제 performance에 의해 반영

▶ 식별 가능성 문제를 해결하기 위해 advantage function이 선택한 action에서 advantage가 0이 되도록 강제
→ 즉, network의 마지막 module이 forward mapping을 구현하도록 구성
▶ 이제 a* = argmax_a'∈A Q(s,a'; θ, α, β) = argmax_a'∈A A(s,a'; θ, α)에서 Q(s, a* ; θ, α, β) = V (s; θ, β)를 얻음
→ 따라서 stream V(s; θ, β)는 value function의 estimate를 제공하는 반면, 다른 stream은 advantage function의 estimate를 생성
▶ 대체 모듈은 max operator를 average로 대체
→ 이는 V와 A가 이제 상수에 의해 목표를 벗어났기 때문에 원래의 의미를 잃지만 최적화 안정성은 증가
→ optimal actions's advantage에 대한 변경을 보상할 필요 없이 평균만큼만 빠르게 변경 가능
▶ 실제로 equation (8)의 softmax version을 사용했지만 아래의 더 간단한 equation (9)과 유사한 결과를 도출하여 해당 논문에서 보고된 모든 실험은 아래의 모듈을 사용

▶ equation (9)에서의 평균을 빼면 식별 가능성에 도움이 되지만 A(따라서 Q) value의 상대적 순위는 변경되지 않고, equation (7)의 Q-value를 기반으로 하는 e-greedy policy가 유지
→ action을 선택할 때 결정을 내리기 위해서는 advantage stream을 evaluate하는 것으로 충분
▶ equation (9)는 별도의 algorithm 단계가 아니라 network의 일부로 보고 구현되다는 점에 유의
→ standard Q-network와 마찬가지로 Dueling network 훈련에는 역전파만 필요
→ estimates V(s; θ, β) 및 A(s, a; θ, α)는 extra supervision or algorithmic modification 없이 자동 계산
→ Dueling architecture는 standard Q-network와 동일한 입출력 interface를 공유하므로 Q network를 사용한 모든 학습 algorithm을 재활용하여 훈련 가능
4. Experiment
▶ 간단한 policy evaluation task로 시작한 다음 일반적인 Atari game 플레이에 대한 더 큰 규모의 결과를 확인
4.1 Policy evaluation
▶ Q-value 학습을 위해 temporal difference 학습(eligibility traces 없이; λ = 0) 사용
→ 구체적으로 behavior policy π가 주어졌을 때, equation (4)의 costs sequence를 최적화 함으로써 state-action value Q^π를 estimate
→ expected SARSA의 같은 방식으로 update를 진행하지만, expected SARSA처럼 behavior policy를 수정하지 않음
▶ 해당 policy evaluation task는 exploration strategy의 선택, policy improvement, policy evaluation 간의 interacion과 같은 교란 요소가 없기 때문에, network architecture를 evaluate하는데 매우 유용
→ 학습된 Q-value를 평가하기 위해 정확한 Q^π(s,a) value가 모든 (s, a) ∈ S × A에 대해 별도로 계산될 수 있는 간단한 환경
▶ Corridor이라고 불리는 환경은 좌하단부터 우상단까지 가장 큰 보상을 얻기위해 이동
→ 사용 가능한 action: 위, 아래, 왼쪽, 오른쪽, 정지
→ behavior policy π로 e-greedy policy를 사용하며 실험에서 e 값은 0.001
▶ single stream Q architecture를 각각 5, 10, 20개의 actions로 corridor 환경의 세가지 변형에 대한 Dueling architecture와 비교
→ 10, 20 action 변형은 원래 환경에 무작동을 추가하여 형성
▶ true state value ∑s∈S, a∈A (Q(s,a; θ) −Qπ(s,a))^2에 대해 Squared Error(SE)로 성능을 측정
▶ single-stream architecture는 각 hidden layer에 50개의 unit이 있는 3 layer MLP
→ Dueling architecture도 3개의 layer로 구성
→ 50개 units의 첫 번째 hidden layer 이후에 network는 각각 25개의 hidden units가 있는 2 layer MLP인 두 개의 stream으로 분기

- 5가지 actions: 두 architecture 모두 거의 같은 속도로 수렴
- 10가지, 20가지 actions: Dueling architecture가 standard Q-network보다 더 나은 성능을 보임
▶ Dueling architecture에서 stream V(s; θ, β)는 s에서 많은 유사한 action에 걸쳐 공유되는 일반적인 value를 학습하므로 더 빠른 수렴으로 이어짐
▶ large action spaces를 가진 많은 control task가 이 속성을 가지고 있기 때문에 매우 유망한 결과이며 결과적으로 Dueling network가 종종 traditional single stream network보다 훨씬 더 빠른 수렴으로 이어질 것으로 예상됨
4.2 General Atari Game-Playing
▶ 57개의 Atari game으로 구성된 Arcade Learning Environment에서 제안한 방법에 대한 evaluation 수행
→ 문제는 raw pixel observations & rewards만 주어진 모든 game을 플레이 하는 방법을 배우기 위해 고정된 hyperparameter set와 함께 single algorithm 및 architecture를 배포하는 것
▶ 이 환경은 매우 다양한 game으로 구성되어 있고, observation이 high-dimensional하므로 매우 까다로움
▶ DQN과 동일한 low-level convolutional structure를 지님
→ 3개의 convolutional layer과 2개의 fully-connected layer 존재
→ Dueling network는 fully-connected된 두개의 stream으로 나뉨
→ value & advantage streams은 모두 512 units의 fully-connected layer를 가짐
▶ value & advantage stream은 모두 하나의 output stream과 valid action이 있는 만큼의 advatage stream과 fully-connected 되어 있음
→ equation (9)에 의해 설명된 모듈을 사용하여 value & advantage stream을 결합
▶ DQN과 같은 optimizer와 hyperparameter를 채택
→ Dueling network에서는 조금 더 낮은 학습률과 value & advantage stream에서 마지막 convolution layer로의 backpropagation gradient을 1/√2만큼 재조정하여 안정성을 증가
▶ gradient clipping하여 norm이 10보다 작거나 같도록 설정
→ clipping은 recurrent network 훈련에서 일반적인 관행
▶ DDQN의 기여도를 독립시키기 위해서 DDQN 또한 위 조건으로 재훈련시키고, 이를 Single이라고 명명
▶ Single에서 gradient clipping을 적용한 모델을 Single Clip이라고 명명
▶ 다음 표는 Single network을 baseline으로한 Dueling network의 개선을 보여줌
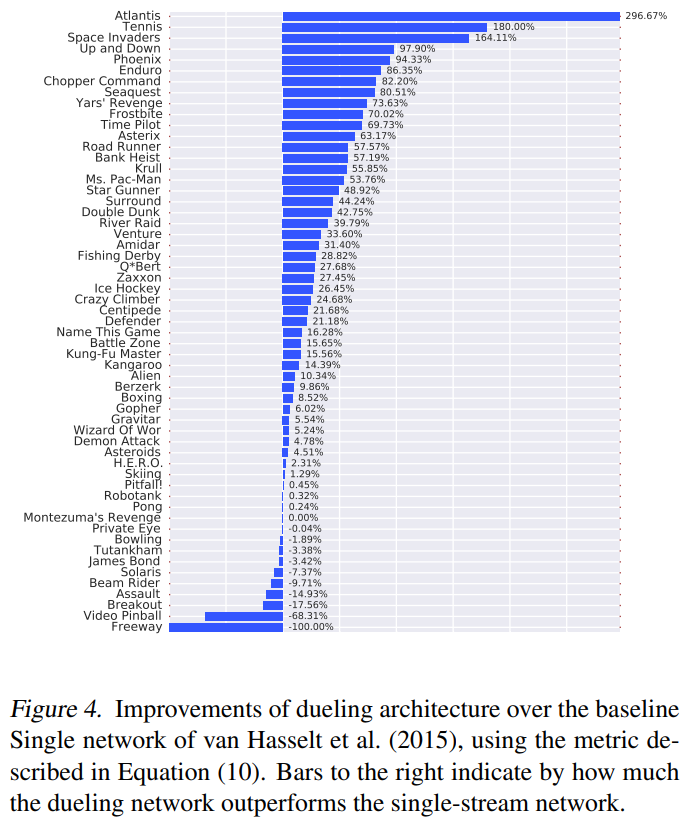
▶ 다음 표는 Single Clip이 Single보다 성능이 좋고, 이러한 이점이 gradient clipping에 의해 가져온 것임을 확인하여 모든 새로운 접근 방식에 통합시킴
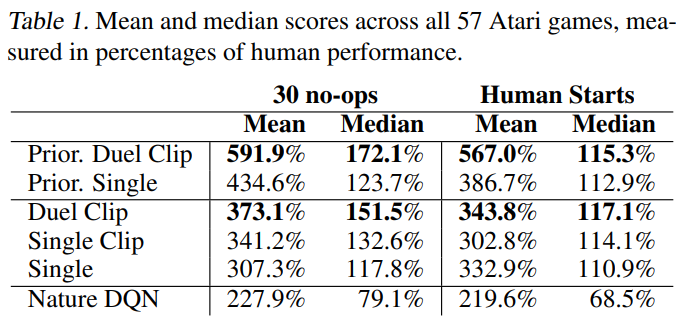
▶ Duel Clip은 Single Clip보다 더 나은 성능을 보이며 Single baseline과 비교하여 더 높은 점수를 달성
(1) Robustness to human starts
▶ 30 no-ops metric의 한가지 단점은 agent가 Atari game을 플레이하기 위해 반드시 잘 일반화할 필요는 없다는 것
→ Atari 환경의 deterministic 특성으로 인해, agent는 고유한 출발점에서 단순히 일련의 actions를 기억함으로써 좋은 성과를 달성하는 법을 배울수 있음
▶ 보다 강력한 측정값을 얻기 위해, 각 game에 대한 인간 전문가의 trajectory에서 sampling된 100개의 starting point를 사용하면 이러한 각 points에서 최대 108,000 frames에 대한 evaluation episode가 시작
→ agent는 starting point 이후에 발생한 reward에 대해서만 evaluate되고 이 metric을 Human Starts라고 명명
(2) Combining with Prioritized experience replay
▶ Dueling architecture는 다른 알고리즘 개선 사항과 쉽게 결합 가능
▶ 특히 prioritization of experience replay는 Atari games의 성능을 크게 향상
또한 prioritization과 Dueling architecture가 학습 프로세스의 매우 다른 측면을 다루기 때문에 둘의 조합이 유망
▶ 다음 표는 prioritized DDQN을 baseline으로한 Dueling network의 개선을 보여줌

▶ prioritized Dueling agent는 prioritized baseline agent와 Dueling agent alone 보다 더 나은 성능을 보임
▶ 결과적으로 prioritized replay와 Dueling network의 조합은 ALE 벤치마크에서 이전의 기술보다 크게 개선
(3) Saliency maps
▶ value & advantage streams의 역할을 더 잘 이해하기 위해 saliency maps를 계산
▶ value stream에 의해 보이는 image의 두드러진 부분을 시각화 하기 위해 input frame에 대한 Jacobian of ^V의 절대값인 다음을 계산

▶ advantage stream에서 볼 수 있는 imgae의 두드러진 부분을 시각화 하기 위해 다음을 계산

▶ 두 quantities 모두 input frame과 같은 차원이므로 input frame과 함께 쉽게 시각화 가능
→ RGB 채널에 대한 배치를 마친 후 image를 형성해보면, time-step에 따른 game의 value & advantage saliency maps를 보여줌
▶ value stream은 자동차의 외관이 future performance에 영향을 미칠 수 있는 지평선과 점수에 주목
▶ advantage stream은 immediate 충돌 코스에 있는 자동차에 주목
5. Discussion
▶ Dueling architecture의 장점은 부분적으로 state-value function을 효과적으로 학습 가능
▶ Q-value가 update될 때마다 value stream V가 update되며, 이는 actions 중 하나의 value만 update되고 다른 모든 action의 값은 그대로 유지되는 single-stream architecture의 update와 대조
▶ value stream을 더 자주 update하면 V에 더 많은 리소스를 할당하므로 state value를 더 잘 approximate할 수 있으며, 결과적으로 이는 Q-learning과 같은 TD-based method가 작동하려면 정확해야 하는데 필요
▶ 이 현상은 single-stream Q-network에 비해 Dueling architecture의 이점인 number of actions가 클 때 더 잘 반영
▶ 여러 games에서 주어진 state에 대한 Q-value 간 차이는 종종 Q의 크기에 비해 매우 작음
→ 이러한 규모의 차이로 인해 update에서 약간의 noise가 발생할 수 있으므로, action이 재정렬되어 nearly greedy policy가 갑자기 발생할 수도 있음
▶ advantage stream이 있는 Dueling architecture는 이러한 효과에 강력
6. Conclusions
▶ 해당 논문에서는 DQN에서 value와 advantage를 분리하는 동시에 common feature learning module를 공유하는 새로운 neural network architecture를 도입
▶ Dueling architecture는 일부 algorithm 개선과 결합되어 Atari domain에서 Deep RL에 대한 기존 접근 method에 비해 극적인 개선을 이루어냄
'논문 리뷰 > 과거 RL 정리' 카테고리의 다른 글
| Semi-supervised classification with GCN (0) | 2022.01.21 |
|---|---|
| Prioritized Experience Replay (0) | 2021.12.29 |
| DDQN(Double DQN) (0) | 2021.12.12 |
| DQN(Deep Q-learning) (0) | 2021.12.11 |
댓글