목차
Combinatorial Optimization
RL method
POMO(Policy Optimization with Multiple Optima)
Optimization in the field
Combinatorial Optimization
Combonatorial Optimization(조합최적화)란?
: 주어진 item들의 최적 순서 또는 매핑(Mapping)을 찾는 문제(ex. 생산 설비 운영 최적화, 자원 할당 최적화, 운송 경로 최적화, ...)이다.
TSP(Traveling Salesman Problem)

: 모든 도시들의 좌표가 주어졌을 때, 가장 최소의 경로로 모든 도시를 이동하는 경로를 찾는 대표적인 조합최적화 예시이다. 모든 경우의 수를 다 해보고 최소 경로를 찾는 것이 최고지만, 경로의 수가 너무 많다.
따라서 최적의 해를 찾기보다는 최적에 가까운 해를 빠른 시간에 찾아내는 방법(Herustic)이 현실적이다.
"Improvement" heuristic
: 일반적인 solution 생성 뒤, 만들어져 있는 조합에서 조금씩 변형을 시도하는 방법이다. 특징은 다음과 같다.
1) 문제가 커질수록 문제 해결에 필요한 시간이 급속도로 증가한다.
2) 좋은 변형/조합 방법은 문제마다 다르기 때문에, 전문가의 tuning이 중요하다.
"Construction" by AI
: 실제 문제를 풀기 전, 비슷한 케이스를 반복해 학습한 다음, 실전에서는 one-shot으로 솔루션을 제공한다. 특징은 다음과 같다.
1) 속도가 매우 빠름
2) 문제마다 새로운 해결 기법의 개발 필요 없이, 데이터에서 스스로 전략을 학습함
RL method
Combinatorial optimization(CO) 문제에서 RL은 NP-hard 문제에 빠르고 강력한 solution을 제공할 수 있다. 상당한 domian 지식을 보유한 전문가 없이도 optimal solution을 찾을 수 있기 때문에 실제 응용 분야에서 큰 잠재력을 지닌다.
1) Supervised Learning
: Computer Vision(CV) 및 natural language processling(NLP)에서 전문가의 수동적 feature engineering은 지도 학습의 발전으로 automated end-to-end deep learning algorithm으로 대체되었다. 그러나 조합최적화 문제에서는 가르쳐줄 정답(optimal label)을 모르는 상태이기 때문에 이러한 지도 학습은 사용이 불가능하다.
2) Reinforcement Learning
: score이 주어지면 학습하는 RL의 패러다임은 대부분의 CO solution에 쉽게 적용될 수 있으며 모델 훈련에 매우 적합하다. 또한 Baseline과의 비교를 통해, 현재의 인공지능의 신경망을 강화 혹은 약화 시킬지 결정한다.
Baseline
: 기본적으로 같은 문제를 여러 번 반복해 풀어서 그 결과의 평균을 사용한다.
인공지능이 반복해 풀어 얻는 solution은 보통 서로 엇비슷하고 크게 다르지 않다. 학습 공간 안에서 Local Optimum에 수렴할 가능성이 높다. 따라서 Global Optimum 발견이 힘들다.
POMO(Policy Optimization with Multiple Optima)
POMO는 modified REINFORCE algorithm을 사용하며, low-variance baseline은 RL 학습을 빠르고 안정적으로 만들어 준다. POMO에서 제공되는 framework는 CO solution의 sequential representation에서 발견되는 CO 자체의 symmetries을 이용하기 때문에 광범위한 general CO 문제에 적용 가능하다. 해당 algorithm은 다음과 같은 크게 세 가지의 컨셉으로 구분할 수 있다.
Identify symmetries
multiple optima로 이끄는 CO 문제를 해결하기 위한 RL method에서 대칭을 식별한다. 이러한 symmetries는 parallel multiple rollouts를 통해 신경망 교육 중에 활용할 수 있으며, 각 trajectory는 서로 다른 optimal solution을 갖는다.
Low-variance baseline
policy gradient에 대한 새로운 low-variance를 고안한다. 이 baseline은 서로다른 trajectories에서 파생되기 때문에 학습은 local minima에 덜 취약하다.
Inference techniques & instance augmentation
기존의 sampling inference method보다 효과적인 multiple greedy rollouts를 기반으로 한 inference method를 제시한다. 또한 inference 단계에서 CO 문제의 symmetries을 추가로 활용할 수 있는 instance augmentation 기술을 소개한다.
Multiple Optima란?

: 경로를 sequence로 출력할 때, 어떤 도시로부터 시작하는지에 따라서 표현할 수 있는 방법이 달라진다. 문제의 Optimum은 하나 인데 표현 방법의 차이로 인해 Multiple Optima가 출력된다.

: 기존의 방법은 인공지능이 한 가지의 최적 경로만 잘 찾도록 학습했지만, POMO는 Multiple Optima로 인위적으로 모든 최적해 경로를 학습하도록 한다. 많은 경우에 CO 문제의 solution은 node sequence로 표현될 때, 여러 형태를 취할 수 있다. 따라서 루프를 포함하는 routing 혹은 set를 찾는 문제는 같은 optimal solution은 다른 sequence로 동일하게 나타내진다.
Precondition
Node group {v_1, v_2, ... , v_M}과 theta로 parameterize된 policy network가 존재한다. i번째 action a_i가 node v_j를 선택할 수 있는 solution T = (a_1, ..., a_M)은 stochastic policy에 따라 한 번에 node 하나씩 신경망에 의해 생성되며 여기서 s는 problem instance로 정의된 상태이다.
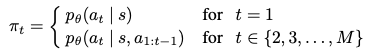
sequence간의 equivalence에 대한 사전 지식을 가진 agent는 어떤 노드를 먼저 출력하기로 선택하든 상관없이 동일한 solution을 생성해야 한다.이 때, 위 방정식에서 볼수 있듯이 initial action a는 어떻든 간에 agent의 나머지 action course(a_2, a_3, ..., a_M)에 큰 영향을 미치게 된다.
1) Explorations from multiple starting nodes
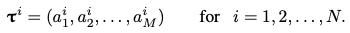
: POMO는 N개의 서로 다른 nodes {a^1_1, a^2_1, ..., a^N_1 }을 exploration의 starting point로 사용한다. network는 N개의 solution trajectories를 MC method를 통해 각 trajectory가 sequence로 정의된다.
기존 RNN에서의 fixed first node로 인한 network가 특정 starting point를 선호하게 되는 START token theme와는 다르게, 모든 first action이 동등하게 좋은 경우 exploration를 개선하기 위한 entoripy maximization을 적용하는 것이 현명하다. START token에서 시작된 trajectory는 single optimal path와 가깝게 유지되지만, POMO의 N solution trajectories는 optimal solution의 N개의 서로 다른 node sequence representation과 밀접하게 일치한다.
개념적으로, POMO의 exploration는 동일한 문제를 여러 각도에서 반복적으로 해결하도록 안내하는 것과 유사하다.
Entropy maximization
: 일반적으로 RL의 objective function에 entropy regularization term을 추가하여 수행된다. 그러나 POMO는 network가 항상 여러 trajectory를 생성하도록 하여 first action에서 entropy를 직접 최대화하여 모든 trajectory가 학습 도중 동일하게 기여하게 한다.
2) A shared baseline for policy gradients
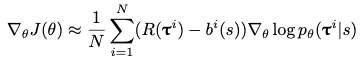
: POMO는 REINFORCEE algorithm을 기반으로 한다. 일단 solution trajectory set {T_1, T_2, ... , T_N}를 sampling하면 , 각 solution T_i의 return R(T_i)를 계산할 수 있다. expected return J를 maximize하기 위해 위 approximation 방정식으로 gradient ascent를 사용한다. 기존 baseline과 다른 특징으로는 서로 다른 시작점에서 문제를 풀도록 한 후, 결과를 종합하여 결정한다는 것이다.
Shared baseline
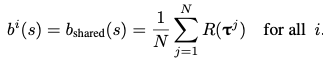
: b_i(s)는 sampling된 gradient의 variance를 줄이기 위한 baseline이다. 원칙적으로는, 각 trajectory T_i에 대해 다르게 할당되는 a^i_1의 함수이다. 그러나 POMO에서는 shared baseline을 사용한다. 이는 이전에 deep-RL 구성 방법에서 사용된 다른 baseline과 비교하여 효율적으로 계산이 가능하다. 결과적으로 POMO baseline은 greedy rollout baseline과 비교하여 policy gradient의 variance를 줄인다.
shared baseline을 사용하지 않았다면 각 sample-rollout T_i는 독립적으로 평가될 것이다. T_i를 생성한 action은 동일한 시작 node a^i_1을 사용하는 greedy-rollout counterpart과의 성능 비교를 통해서만 강화될 것이다. 이 training method는 밀접하게 관련된 두 network에서 생성된 두 roll-out 간의 차이에 따라 진행되기 때문에 actor와 critic 모두 비슷한 method로 실적이 저조한 상태에서 조기에 수렴할 가능성이 존재한다. 그러나 shared baseline을 사용하면 각 trajectory가 N-1개의 다른 trajectories와 경쟁한다. 평가하는 trajectories의 수가 증가하면 모두 적절한 수준에서 baseline을 설정하는데 기여하므로 조기에 수렴하는 현상이 감소하게 된다.
결과적으로 shared baseline은 local minuma에 강한 내성이 있다.
shared baseline method를 사용하며 algorithm1은 mini batch로 학습을 제공한다.

3) Multiple greedy trajectories for inference
CO 문제에 대한 construction type neural network model에는 일반적으로 greedy와 sampling의 두가지 inference mode가 존재한다. sampling된 solution은 평균적으로 greedy solution보다 작은 보상을 반환할 수 있지만, sampling은 computational cost으로 필요한 만큼 반복할 수 있다. sampling된 solution이 많으면 greedy-rollout보다 보상이 더 큰 solution을 찾을 수 있다.
Greedy mode
: policy에서 argmax를 사용하여 single deterministic trajectory를 그린다.
Sampling mode
: probabilistic policy에 따라 network에서 여러 trajectories를 sampling한다.
그러나 POMO의 multi-starting-node 접근 방식을 사용하면 하나가 아닌 여러개의 greedy trajectories를 생성할 수 있다. sampling mode의 접근 방식과 유사하다. N개의 greedy trajectories는 대부분의 경우 N개의 sampling된 trajectories보다 우수하다.
POMO's multi-greedy inference method의 한가지 단점은 N, 즉 사용할 수 있는 greedy rollouts의 수가 유한한 starting-node의 수로 제한되기 때문에 임의로 클 수 없다. 그러나 특정 유형의 CO 문제의 경우에는 instance augmentation을 사용하여 이 제한을 극복할 수 있다.
Instance Augmentation
: 문제 자체를 대칭/회전 변환하여 인공지능이 보기에 새로운 문제를 만들어 제공할 수 있다. 좌표만 바꿨을 뿐이지만, 인공지능이 풀 때는 완전히 다른 계산이 필요하다.
algorithm2는 instance augmentation을 포함한 POMO의 inference method를 설명한다.

Experiments
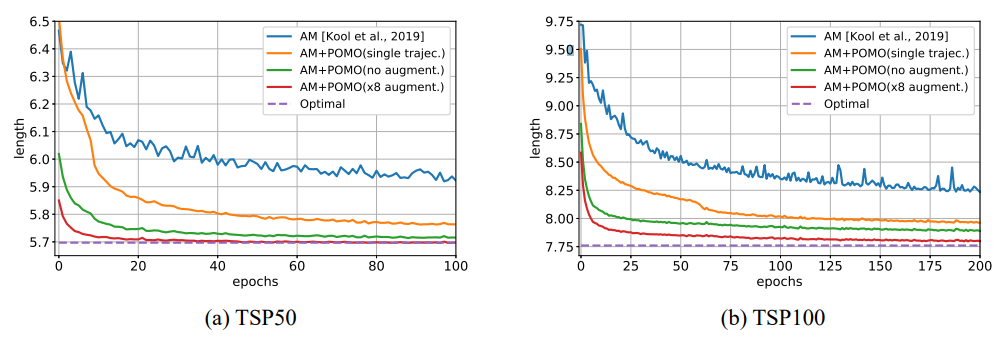
*1 epoch = 100,000개의 random 문제 학습
AM: 전통적인 강화학습 방법
AM+POMO(single trajec.)
AM+POMO(no augment.)
AM+POMO(x8 augment.): AM+POMO 적용 방법
Optimal: 최적의 해
모든 조합 최적화 문제가 Multiple Optima 특성을 가진 것은 아니지만, 거의 대부분의 문제가 이를 보유한다. 이를 이용하면 강화학습 사용시 굉장히 큰 이점을 얻을 수 있다.
Optimization in the field
Abstract problem
생산 설비 최적화
: 생산 순서가 있는 공정을 거치는 경우, 스케줄링 최적화를 통해 제작 시간 감소가 가능하다.
자원 할당 최적화
: 클라우드 컴퓨터에서 프로그램을 사용하는 경우, 공유된 자원의 할당 최적화를 통해 효율적인 시간 관리가 가능하다.
운송 경로 최적화
: TSP와 유사하지만, 중간에 창고가 존재하고 각 지점으로 지정된 할당량을 배송하는 경우에서의 최적 경로를 파악 가능하다.
* 제약 사항: 한 트럭에 실을 수 있는 제품의 양
Optimization in the field
: env가 아닌 현실에서의 강화 학습 적용은 또 다른 문제이다. 위 운송 경로 최적화 예제를 현실에서 적용하게되면 많은 제약 사항들이 발생하게 된다.
운송 경로 최적화
: 가상의 환경에서보다 훨씬 더 많은 제약 사항들이 존재하지만, env에서의 수정을 통해 제약 사항을 포함하게만 해준다면 인공지능이 제약 사항을 적용하여 강화학습이 가능하다.
* 제약 사항: 한 트럭에 실을 수 있는 제품의 양, 다양한 종류의 트럭, 요청 배송 시간대, 왕복 포함 최대 지점 수 제한, ...
Step-by-step
: 사업 현장으로의 강화학습 적용에는 단계적인 방식이 필요하다.
기존 알고리즘과의 좋은 궁합 필요
1) 처음부터 모든 최적화를 AI로 대체하기 보다는, 부분 적용을 고려
2) 기존 알고리즘에서 단순 반복 처리하는 부분의 강화(묶음 만들기, 처리 순서 정하기, Improvement를 위한 starting point 정하기, ...)
학습에 유리한 환경 필요
1) 학습을 위한 Simulator 구축 필요
2) 효과적이고 빠른 학습을 위한 조건들(definite score definition, rapid score calculation, diverse experiment data, ...)
Reference
https://arxiv.org/pdf/2010.16011.pdf
https://www.youtube.com/watch?v=Dyp9lQpVgCs
'개인 정리 > 개념 정리' 카테고리의 다른 글
| Attention Is All You Need (0) | 2022.03.11 |
|---|---|
| Deep RL Policy-based Method (0) | 2022.03.04 |
| Deep RL Value-based Methods (0) | 2022.03.03 |
| Traditional RL (0) | 2022.03.02 |
| Model-free RL, Model-based RL (0) | 2022.02.07 |
| GNN, GCN (1) | 2022.01.21 |




댓글