목차
RL Framework - Problem & Solution
Dynamic Programming
- System of Euqation Method
- Iterative Method
- Policy Evaluation
- Policy Improvement
- Policy Iteration
- Value Iteration
Monte Carlo Methods
Temporal Difference Methods
RL in Continuous Space
RL Framework - Problem
Reinforcement Learning이란?

: agent가 env와의 interaction을 통해서 학습하는 방식이다. initial state S_0에서 action A_0을 하면 env는 new state S_1, new reward R_1을 가지게 되고, 해당 state에서 새로운 action A_2를 선택하는 구조를 반복하며 interaction한다. 이는 sequential하게 S_0, A_0, R_1, S_1, A_1, R_2, S_2, A_2,...와 같이 표현될 수 있다.
Agent's goal
: 강화학습의 목표는 expected cumulative reward를 maximize하는 것이다. 이 때, agent마다 각각 추구하는 goal이 모두 다를 수 있다.(ex. 자율주행 자동차의 경우 drive, 게임일 경우 win, 로봇일 경우 walk)
reward hypothesis

: 모든 goal은 expected cumulative reward의 maximization으로 여겨진다.
R_1 + ... + R_t: past reward
R_(t+1): immediate reward after current action A_t
R_(t+1) + R_(t+2) + ... : future reward
definition of G_t

: 강화학습의 특징은 과거의 reward가 아닌 미래의 reward에 집중한다. 따라서 G_t를 정의할 때, immediate reward부터 미래의 reward만을 포함한다.
discounted return gamma

: 미래의 reward에 gamma 만큼의 discount를 계산하겠다는 의미이다. * γ ∈ [0, 1]
One step dynamics
: one-step dynamics, 즉 state transition에 대한 설계를 위해 action space, state space에 대한 파악이 필요하다.
action space: 각각의 action의 집합
state space: 각각의 state의 집합
trash cleaner robot example
: current battery level을 state로 하는 robot일 경우, A = [search, recharge, wait], S = [high, low]와 같이 space를 표현할 수 있고, state transition은 다음과 같다.

MDP(Markov Decision Process) definition
: finite MDP는 다음의 요소들로 정의된다.
agent knows
- a (finite) set of states S
- a (finite) set of actions A
- a discount rate gamma ∈ [0, 1]
agnet doesn't know
- a (finite) set of rewards R
- the one-step dynamics of the env; p(s', r | s, a) = P(S_(t+1) = s', R_(t+1) = r | S_t = s, A_t = a)
이 때, probability는 오직 current state & current action에 영향을 받는다. 과거의 states, actions, rewards는 고려하지 않는다는 것이 MDP의 특징이다.
RL Framework - Solution
Policy; pi
deterministic policy

: state를 input으로 했을 때, output으로 action이 바로 나온다.
stochastic policy

: state & action을 input으로 했을 때, output으로 action probability가 나온다.
State-value function; v_pi(s)

: policy pi를 기반으로 state s에서의 value를 의미한다. 현재 state부터 기대되는 return이며 state에 대한 평가이다. 아래는 수식으로 표현한 state-value function이다.
v_pi(s) = E_pi[G_t|S_t = s]
: state s를 시작으로, policy pi를 기반으로 모든 time steps에서 action을 선택한 expected return를 의미한다.
Bellman Equation

: 쉽게 표현하자면 current state-value function = immediate reward + discounted gamma * next state-value function이다. 이는 모든 state에서 적용된다.
Bellman Expectation Equation

Bellman Equation Back-up diagram

: state-value funtion v_pi(s)는 다음 action-value function의 policy에 기반한 가중평균으로 이해할 수 있고, action-value function q_pi(s, a)는 다음 state-value function에 대한 reward와 state transition probability의 가중평균으로 이해할 수 있다. 따라 Bellman Equation을 풀면 각 state, action에 대한 value 판단이 가능하다.
Bellman Optimality Equation
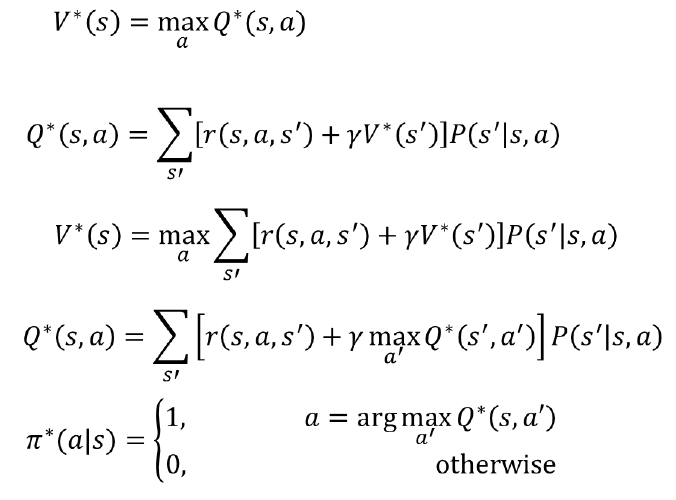
Bellman Optimality Equation Back-up diagram

: Bellman Equation과 다르게 여기서는 가중평균이 아닌 최대값의 방향으로 action을 선택하는 것이 차이점이다. optimal state-value function은 다음 action-value function 중 최대가 되는 쪽으로 back-up diagram이 이동하고, action-value fuction은 다음 state-value function의 최대값에 대한 가중 평균이다.
Optimal policy; pi*
: optimal policy pi*는 value function들을 공유한다. 즉, 여러 개의 optimal policy가 있다고 하더라도 value function은 동일하다는 뜻이다.
v_pi'(s) >= v_pi(s) for all s ∈ S
: pi'의 모든 state-value function이 pi의 모든 state-value function보다 큰 경우에 더 좋은 policy라고 할 수 있다. 비교 도중, 두 개의 policy의 판단이 어려운 경우가 종종 있을 수 있다.
v_pi* >= v_pi for all pi
: 결국 optimal policy란 모든 pi들 중 가장 좋은 policy를 의미한다. optimal policy는 존재가 보장되지만, unique하지 않을 수도 있다.
v*
: v_pi*에 기반한 optimal state-value function를 의미한다.
q*
: q_pi*에 기반한 optimal action-value function를 의미한다.
Action-value function; q_pi(s, a)
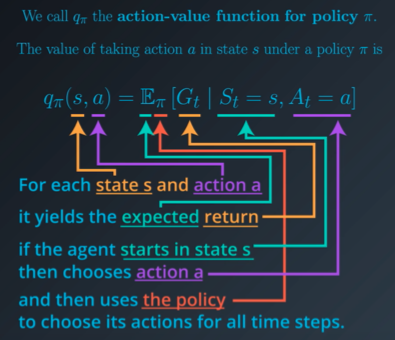
: policy pi를 기반으로 state s에서 action a를 선택했을 때의 value를 의미한다. 현재 state가 주어지고 현재 action으로부터 기대되는 return이며 action에 대한 평가이다. 아래는 수식으로 표현한 action-value function이다.
q_pi(s, a) = E_pi[G_t|S_t = s, A_t = a]
: state s에서 action a를 선택했을 때를 시작으로, policy pi를 기반으로 모든 time steps에서 action을 선택한 expected return를 의미한다.
결과적으로 optimal action-value function q*을 구했을 경우, optimal policy pi*를 계산할 수 있다. 결국 우리는 optimal action-value function을 구하기만 하면 된다.
TRL - Dynamic Programming
: DP method는 agent가 MDP에 대한 모든 지식을 알고 있다고 설정한다. 즉, state, action, discount factor 이외에도 rewards, state transition까지 모두 안다고 가정한다.
System of Equation Method
: 각각의 value-function을 구하기 위해 연립방정식을 사용했지만, 현실 세계에서는 state, action space의 크기로 인해 calculation이 불가능하여 다른 방식들이 도입되었다.
Iterative Method

: 지속적으로 calculation을 진행하여 optimal state-value function에 수렴할때까지 반복하는 방식이다. MDP를 모두 알고 있는 방식이기에 가능하다. 연립방정식으로 풀 수 없는 것을 iterative method로 일반적으로 해결할 수 있다.
Policy Evaluation(Prediction)

: iteration을 언제까지 반복시켜야 하는가에 대한 값을 정해주는 방식이다. small positive number(hyperparameter) theta를 두고 value의 변화량이 theta보다 작으면 iteration을 멈추는 알고리즘이다. state-value function을 return한다.
Policy Improvement(Control)

: state-value function v로 action-value function q를 구한 뒤, arg max Q(s, a)로 policy pi'를 구하는 과정이다. pi'을 return한다.
Policy Iteration

: policy evaluation과 policy improvement를 반복하는 방식이다. 이 역시도 무한정 반복할 수 없기 때문에, policy evaluation에서 small positive number theta를 사용하고, state-value function V를 return한다. policy improvement에서는 evaluation의 결과인 state-value function V를 input으로 하여 policy pi'을 return한다.
Truncated Policy Iteration

: 과도한 computation을 방지하고자 policy iteration을 적당한 구간에서 언제 멈출 것인지 결정해주는 방식이다.
Value Iteration

: Bellman Optimality Equation을 사용하여 arg max를 사용하므로 policy pi의 영향을 받지 않는 방식이다. transition 후 value를 계산해보고 policy를 update한다.
Policy iteration vs. Value iteration

Policy iteration
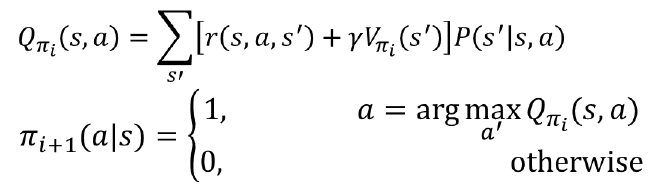
1) Bellman Expectation Equation을 이용하여 Policy evaluation 과정에서 state-value function V를 구한다.
이 때, evaluation과 improvement가 1번씩 번갈아 가면서 진행되는 것이 아니라, V_pi에 수렴할 때까지 evaluation을 진행한다. 즉, state-value function이 더 이상 바뀌지 않을 때까지 evaluation을 진행한다. (한번만 evaluation만 진행할 수도 있다.)
2) state-value function V로 action-value function Q를 구해 가장 큰 쪽으로 Policy improvement를 하여 pi'를 구한다.
3) Policy evaluation과 Policy improvement를 위 방식대로 반복하여 value function의 변화가 없을때까지 policy를 update한다.
Value iteration

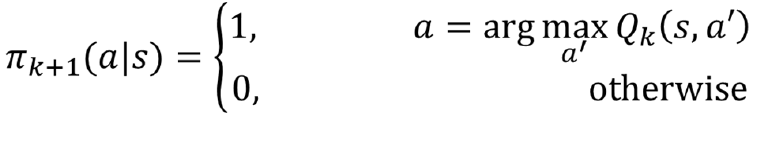
1) Bellman Optimality Equation을 이용하여 state-value function을 구한다.
이 때, max를 사용하기 때문에 policy pi의 영향을 받지 않는다.
2) state-value function에 max 값을 구해 value가 가장 큰 쪽으로 policy를 update한다.
3) 위 방식을 번갈아가며 반복하여 policy를 update한다.
결국, 두 방식 모두 같은 수렴점을 향해 다가간다.
TRL - Monte Carlo Method
MC method란?

: agent가 state, action, reward로 이루어진 sequence episode를 terminate 될 때까지 진행하는 방식이다. 전체 episode를 다 알아야 해당 state의 action-value function을 구할 수 있다. episode 종료 시, reward의 expected cumulated return G_t를 구할 수 있다.
1) DP와 다르게 MC의 agent는 reward와 state transition에 대해 알 수 없다. 따라서 실제로 experience를 해보고, env가 준 정보를 통해 optimal policy pi*를 구하기 위해 optimal state-value function v*, optimal action-value function q*을 구해야 한다.
2) episode가 많아야 모든 action-value function q를 구할 수 있다. 결국 Q-table를 채우기 위해 모든 state와 action의 value function을 구해야만이 optimal policy를 구할 수 있다. 만약, state & action space가 크다면, 너무 많은 episode가 요구된다.
3) 초기에는 random policy로 진행하지만 episode가 쌓이면서 value-function 계산을 하게 되면 policy improvement가 이루어 진다.
Policies
: 아래의 policy를 잘 사용하면 효과적인 exploration, exploitation을 하며 episode를 진행할 수 있다. exploration은 더 많은 정보를 얻기 위한 탐색, exploitation은 현재 얻은 정보에서의 최적의 결정을 의미한다.
Greedy policy
: Q-table에서 action-value function이 가장 큰 action을 선택하는 방식이다.
Epsilon-Greedy policy
: 0-1 사이의 epsilon 값만큼의 확률로 random하게, 1-epsilon 만큼의 확률로는 greedy하게 action을 선택하는 방식이다. RL에서의 exploration-exploitation dilemma를 해결한다.
TRL - Temporal Difference
TD method란?

: episode 내 1 time-step이 끝날 때마다 update를 진행하는 방식이다. current estimate를 update 하기 위해, alternative estimate를 사용한다.
TD - Sarsa

Sarsa
: on-policy 방식이다. next_state에서의 action을 선택하는 값(Q(S_(t+1), A_(t+1))을 e-greedy policy로 가져오는 방식이다.
SarsaMax(aka Q-learning)
: off-policy 방식이다. Q-table의 max 값을 가져온다.
Expected Sarsa
: on-policy 방식이다. summation을 사용한다.
RL in Continuous Space
위에서 설명한 방식들은 기본적으로 discrete space에서의 RL을 기반으로 한 방식들이었다. 그러나 실제로 우리가 접하는 문제들은 continuous space에서 동작한다.(ex. robot, auto driving, ...)
model-based learning(Dynamic programming)
: policy iteration, value iteration
model-free learning
: Monte-Carlo method, Temporal Difference method
Dealing with Continuous Spaces
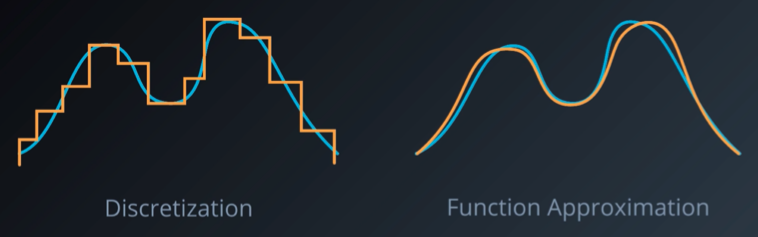
Discretization
: continuous space를 이산화해서, 기존의 discrete space에서의 RL 방식을 사용한다.(ex. discretization, non-uniform discretization, tile-coding, coarse-coding, ...)
Function Approximation
: deep learning을 사용하여 continuous space에서의 새로운 RL 방식을 사용한다. (ex. linear function approximation, non-linear function approximation, ...)
Reference
https://www.youtube.com/watch?v=srgNJWVgs9w&list=PLMhvUUCFLfI4K_d9lCXtY0e3iAEV_HbnK&index=1&t=67s
https://imjuno.tistory.com/entry/Policy-Value-Iteration
Dynamic Programming : Policy Iteration & Value Iteration
Dynamic Programming : Policy Iteration & Value Iteration 돌아서면 까먹는 미래의 나를 위해.... 다시 보아도 바로 이해할 수 있도록 정리한다. MDP가 뭐였지? Markov Decision Processes는 Total Reward를 최..
imjuno.tistory.com
Markov Decision Process (2) - Bellman Equation
이번 포스팅에서는 저번 포스팅에서 살펴본 Value function과 Bellman Equation, 그리고 행동전략인 정책 (Policy)을 정의하여 MDP를 푸는 방법을 살펴보고 강화학습의 뼈대인 MDP를 마무리하도록 하겠습니
yjjo.tistory.com
'개인 정리 > 개념 정리' 카테고리의 다른 글
| Attention Is All You Need (0) | 2022.03.11 |
|---|---|
| Deep RL Policy-based Method (0) | 2022.03.04 |
| Deep RL Value-based Methods (0) | 2022.03.03 |
| Combinatorial Optimization by POMO (0) | 2022.03.01 |
| Model-free RL, Model-based RL (0) | 2022.02.07 |
| GNN, GCN (1) | 2022.01.21 |




댓글