Proceedings of the 35th International Conference on Machine Learning, PMLR 80, 2018
Abstract
: centralized end-to-end method로 decentralized policy를 훈련하는 value-based approach인 QMIX를 제안한다. 이 network는 local observation에만 의존하는 agent 별 value의 complex non-lonear combination으로 joint action value를 추정한다. 구조적으로 joint cation value가 agent 당 value에서 monotonic하게 적용되도록 하여 off-policy 학습에서 policy 간 일관성을 보장한다.
Introduction
: 이전 VDN과 COMA에서의 approach였던, Q_tot를 individual value function Q_a의 sum으로 표현 가능하다는 전제에서 출발한다. 그러나 VDN은 종종 학습 중 많은 extra state 정보를 무시하고 표현되는 centralized action-value function의 complexity로부터 제한된다.
- 해당 논문에서는 action-value function의 더 풍부한 표현인 QMIX를 제안한다.이는 곧, VDN의 full factorisation이 decentralized policy를 추출하기 위해 필요하지 않다는 의미가 있다. 대신 우리는 Q_tot에서 수행되는 global argmax가 각 Q_a에서 수행된 individual argmax action set와 동일한 결과를 산출하는지 확인하기만 하면 된다. 이를 위해, Q_tot와 Q_a 사이의 관계에 monotonous constraint를 적용하는 것으로 충분하다.
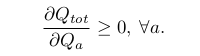
- QMIX는 각 Q_a를 나타내는 agent network와 centalized와 decentralized policy 간의 일관성을 보장하는 complex non-linear method로 Q_tot로 결합하는 mixing network로 구성된다. 동시에 mixing network가 positive weight는 갖도록 제한하여 위 constraint condition을 적용한다.
→ 결과적으로 QMIX는 agent 수에 따라 잘 확장되고 linear-time individual argmax operation을 통해 decentralized policy를 쉽게 추출 가능한 factoring representation으로 complex centralized action-value function을 나타낼 수 있다.
- Algorithm은 CTDE method로 동작하며, 학습 도중에는 local action observation histories T와 global state s에 접근 가능하지만, 각 agent's learnt policy는 own action-observation history T^a에만 조건한다.
QMIX
: VDN과 마찬가지로 IQL, centralized Q-learning 사이에 있지만 훨씬 더 풍부한 action-value function을 나타낼 수 있는 QMIX approach를 제안한다. centralized policy와 완전히 일치하는 decentralized policy를 추출하기 위해서는 더이상 VDN의 full factorisation이 필요하지 않다. 대신 일관성을 위해, Q_tot에 대해 수행된 global argmax가 각 Q_a에 대해 수행된 individual argmax action set와 동일한 결과를 산출하도록 보장하면 된다.

- 이를 통해 각 agent a는 Q_a와 관련하여 greedy action을 선택함으로써 decentralized execution에 참여할 수 있다. 만약 위 equation이 만족되면 policy 외 학습 update에 필요한 Q_tot의 argmax를 취하는 것은 다루기 쉽다.
→ VDN에서의 Q-tot factorisation을 기반으로 하여 더 풍부한 action-value function을 나타내기 위한 approach를 제안한다.
- VDN으로 위 equation을 만족시키기에 충분하지만, QMIX에서는 이러한 조건은 더 큰 범위에서 monotonous function로써 표현이 가능하며 Q_tot와 각 Q_a 사이의 관계에 대한 아래의 constraint가 성립될 경우 일반화될 수 있다는 것을 기반으로 한다.

- 위 constraint 수행을 위해 agent network, mixing network, set of hypernetwork를 사용하여 Q_tot을 나타낸다.

- 각 agent a에 대해 각 time-step에서 input으로 individual observation o와 last action u^a_t-1을 받는 DRQN으로 individual value function Q_a(τ_a, u_a)를 나타낸다.

- Mixing network는 agent network output를 input으로 받아 monotonically 혼합하여 Q_tot value를 생성한다. monotonicity constraint를 시행하기 위해 mixing network's weight는 non-negative로 제한된다. 이는 mixing network가 임의의 monotonic function에 근접하는 것을 허용한다.
- Mixing network's weight는 별도의 hypernetwork에서 생성된다. 각 hypernetwork는 state s를 input으로 사용하고 mixing network의 각 layer wieght를 생성한다. 각 hypernetwork는 mixing network weight가 non-negative임을 보장하기 위해 single linear layer와 absolute activation function으로 구성된다. 그 결과, hypernetwork's output는 적절한 크기의 matrix로 재구성되는 vector이다. bias는 동일한 방식으로 생성되지만 non-negative로 제한되지 않는다. final bias는 ReLU non-linearity가 있는 2-layer hypernetwork에 의해 생성된다.

→ 아래 그림의 붉은색 부분이 hypernetwork이고 state를 input으로 각 layer 마다 non-negative weight인 파란색 부분을 생성하여 mixing network를 구성한다.
- Q_tot는 non-monotonic하게 extra state 정보에 의존할 수 있기 때문에, state는 mixing network로 직접 전달되지 않고 hypernetwork에서 사용된다. 따라서 agent 당 value와 함께 monotonic network를 통해 state function을 전달하는 것은 제한적이게 된다.
→ hypernetwork를 사용하면 임의의 방식으로 monotonic network's weight를 s로 조정할 수 있으므로, global state s를 joint action-value estimate에 통합할 수 있다.
- QMIX는 end-to-end 방식으로 다음의 loss를 최소화하기 위해 학습한다. 이는 표준 DQN loss와 유사하다. b는 replay buffer의 batch size이고, θ-는 DQN target network parameter를 의미한다.

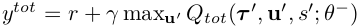
→ Q_tot의 분해 성질이 성립하기 때문에 agent 수에서 linear time에 Q_tot 최대화를 진행 가능하다.
Representational complexity
: QMIX로 표현할 수 있는 value function class에는 fully observable setting에서 agent's individual value function이 non-linear monotonic combination으로 factored 가능한 모든 value-function이 포함된다. 이는 VDN으로 표현되는 linear monotonic value function을 확장한다.
- 그러나 constraint condition은 QMIX가 이러한 방식으로 factorise 하지 않는 value function을 나타내는 것을 방지한다. 직관적으로 agnet's best action이 같은 time-step에서 다른 agent's action에 의존하는 value function은 적절하게 분해되지 않으므로 QMIX로 완벽하게 표현할 수 없다. 그러나 QMIX는 이러한 value function을 VDN보다 더 정확하게 근사가 가능하다. 도한 경험적으로 보여주는 훈련 중에 사용할 수 있는 extra state 정보를 활용할 수도 있다.
→ 내용이 더 있으나 이해하지 못했다.
QMIX example
: VDN과 QMIX의 representational complexity effiect를 설명하기 위해 두 agent에 대한 간단한 2-step cooperative matrix game을 고려해본다.

1. agent 1은 두 가지 matrix game 중 다음 step에서 실행할 game을 선택한다.
: 첫 번째 step에서는 agent 2's action이 효과가 없다.
2. 두 agent는 table 1에 나와있는 payoff matrix에 따라 action을 선택하고 global reward를 받는다.
- Full exploration은 각 method가 궁극적으로 사용 가능한 모든 game state를 explore하도록 보장하여 state-action value function의 representational 능력이 유일한 constraint로 남도록 한다.
- Table 2는 학습된 Q_tot value를 보여주고, VDN보다 QMIX에서 joint action value function를 더 정확하게 표현한다.

QMIX results
: Rich set of complex micro actions를 포함한 competitivae와 cooperative multi-agent problem을 가지고 있는 StarCraft 2 Micromanagement env(SC2LE)에서 실험을 진행한다.
Decentralised StarCraft II Micromanagement
: 각 agent는 individual army unit을 각각 통제하며, move[direction], attack[enemy id], stop, and noop의 discrete action space를 가진다. direction에는 4방향으로만 움직일 수 있고, unit은 적이 shooting range 안에 있다면 attack[enemy id]이 가능하다. 추가로 unit sight range로 인해 partial observability가 달성된다. joint reward는 적에게 입한 total damage와 추가로 킬당 point, 모든 적 섬멸에 200 point로 설정하였다.
- 모든 scenario에서 IQL은 다른 agent들의 action changing으로 인한 env non-stationary 때문에 highly unstable하여 적을 이기는 policy를 갖지 못하였다.
- joint action-value function을 배우는 이점은 IQL를 뛰어넘는 VDN의 performance를 보면 나타나진다. VDN은 focus firing의 형태로 basic coordinated behaivor이 가능했지만 3m(marine) episode에서는 의미있는 성과를 내지 못했다.
- QMIX는 모든 episode에서 주목할만한 performance를 보였으며 하위 3개의 episode에서 다른 algorithm과 큰 격차를 보였다.

Ablations
: extra state 정보의 포함과 mixing network에서의 non-linear transformations의 필요성을 실험해본다.
1. Extra state 정보 포함 유무에 대한 비교
: Mixing network에서 weights와 bias를 기존 방식대로 state에 조건하지 않는 QMIX-NS와 비교한다.
2. Non-linear mixing의 필요성 비교
: Mixing network의 내부 hidden layer를 제거하여 VDN extension의 일종으로 만든 QMIX-Lin과 비교한다.
3. Non-linear mixing과 비교하여 state s를 활용하는 것에 대한 비교
: Agents' Q-value sum에 state-dependent term을 추가하여 VDN을 확장하는 VDN-S와 비교한다. 이 state-dependent term은 state s를 input으로 하는 single hidden layer-ReLU non-linearity가 있는 network에 의해 생성된다.(QMIX에서 final bias를 생성하는 hypernetwork와 동일)
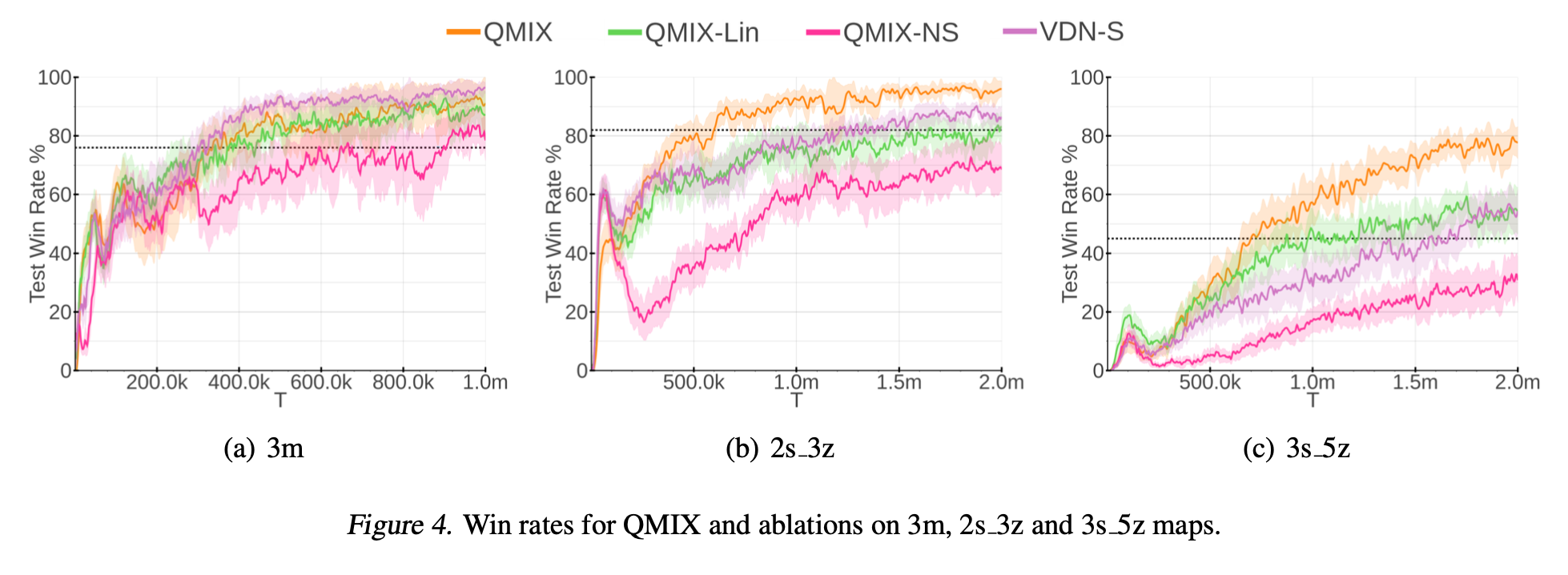
- 위 그림 (a)에서는 non-linear value function factorisation이 homogeneous agent types에서 항상 필요한 것은 아님을 보여준다. 그러나 extra hidden layer을 통해 도입된 추가 complexity가 학습 속도를 늦추진 않는다.
- 위 그림 (b), (c)는 heterogeneous agent types에서 central state 정보와 non-linear value function factorisation이 좋은 성능을 달성하는데 필요함을 보여준다.
→ QMIX-NS는 두 scenario 모두에서 VDN과 동등하거나 조금 더 좋은 성능을 보이며, 이는 복잡한 scenario에서 central state를 조건화하지 않을 때 non-linear decomposition이 항상 유익하지 않다는 것을 시사한다. 또한 QMIX-Lin과 비교한 VDN-S의 성능은 central state 정보를 최대한 활용하기 위해 non-linear mixing의 필요성을 보여준다.
Conclusion
: 해당 논문에서는 centralized env에서 decentralized end-to-end 학습을 허용하고 extra state 정보를 효율적으로 사용하는 QMIX를 제안한다. QMIX를 사용하면 agent 별 action-value function으로 다루기 쉬운 분해를 허용하는 rich joint action-value function을 학습할 수 있다. 이는 mixing network에 monotonicity constraint를 부과함으로써 달성된다. 이는 다른 value-based multi-agent method보다 더 뛰어난 individual Q-learning 뿐만아니라 최종 performance까지 향상시킬 수 있다.
댓글