[Submitted on 16 Jun 2017]
Abstract
: single joint reward signal을 사용하여 cooperative multi-agent RL problem을 연구한다. fully centralized and decentralized approach에서 가짜 reward problem과 partial observability로 인해 발생하는 'lazy agent' 현상을 찾는다. team value function을 개별 agent value function으로 분해하는 network architecture로 개별 agent를 학습시키는 method를 제안한다.
Introduction
: 원칙적으로 cooperative MARL problem은 centralized approach를 사용하여 처리될 수 있으나, 실제로 상대적으로 단순한 problem에서 일관되게 실패한다는 것을 발견했다. 하나의 agent만 활성화되고 다른 agent들은 'lazy'한 상태에서 비효율적인 policy를 학습하게 된다. 이는 한 agent가 유용한 policy를 학습했지만 다른 agent는 첫 번째 agent를 방해하고 더 나쁜 team reward로 이어질 수 있으므로 권장되지 않는다.
- 해결을 위해서 independent learner의 성능을 향상 시키는 개별 agent's observation보다 직접적으로 관련된 개별 reward function을 설계하는 것이다. 그러나 single agent에서도 reward 설정이 어렵고 형성되는 reward function의 작은 클래스만이 진정한 true objective optimality를 보장한다. 해당 논문에서는 team value function의 분해를 토해 일반적인 자율 solution을 학습하는 것을 목표로 한다.
- 암시적으로, value decomposition network는 개별 component value function를 나타내는 neural network를 통해 전체 Q-gradient를 역전파하여 team reward signal에서 optimal linear value decomposition을 학습하는 것을 목표로 한다. 이 additive value decomposition은 independent agent에서 나타나는 가짜 reward signal를 회피한다는 의미가 있다.
→ 일반적으로 multi-agent RL에서 우리는 partial observability로 인해 own action이 reward function에 어떤 영향을 끼쳤는지 알 수 없어 비효율적인 policy 학습을 방지하기 위해 team value function의 분해를 통해 일반적인 policy를 학습하고자 한다.
Deep-RL architecture for coop-MARL
: Purely independent DQN-style agent를 기반으로 하여 개선사항을 추가한다. value decomposition의 기여는 아래 network로 설명된다.


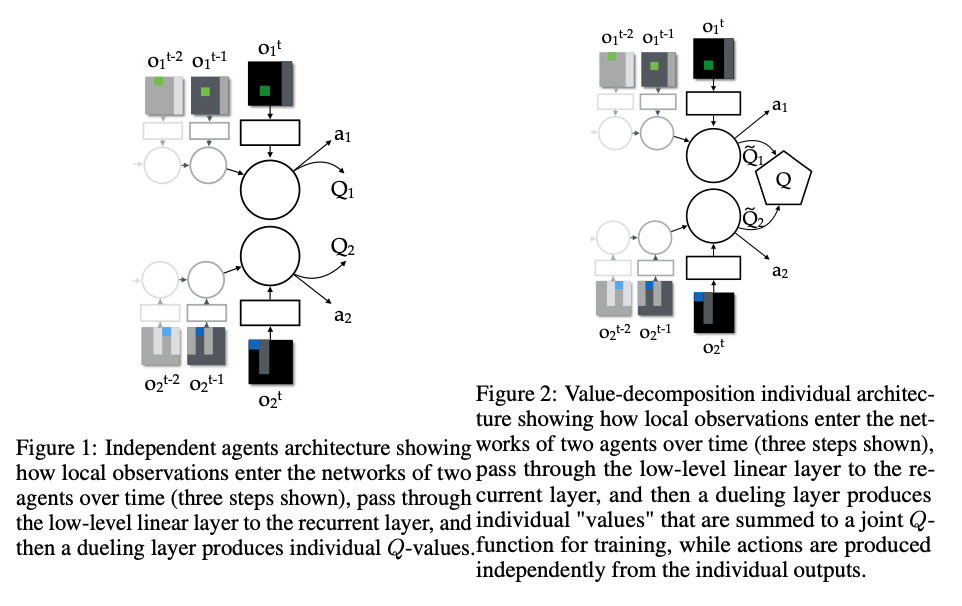
- system에 대한 joint action value function이 agent 전반에 걸쳐 value function으로 분해가 가능하다는 가정을 염두에 둔다. 이 때, ~Q_i는 각 agent's local observation에 depend한다.

- summation을 통해 joint reward를 사용하는 Q-learning rule에서 gradient를 역전파하여 ~Q^i를 학습한다. 즉, agent i에 특정 reward가 아닌 암시적으로 학습되며 ~Q_i가 특정 reward에 대한 action value라는 제약을 부과하지 않는다.
→ agents' summed reward로 network가 update되며, 이 때 각 network의 ~Q-value가 각 agent의 특정 reward에 대한 action value가 아니다.
- value decomposition layer의 속성은 학습에 약간의 centralization이 필요하지만 각 agent가 local value ~Q_i에 대해 greedy하게 행동하기 때문에 학습된 agent를 독립적으로 배포할 수 있다는 것이다.
→ local value ~Q_i에 대해 greedy하게 행동하는 각 agent는, ∑~Q_i를 최대화하여 joint action을 선택하는 central arbiter와 동일하다고 볼 수 있다.
at Dueling layer
- 2개의 agent가 있는 경우, agent observation에 reward가 가산적으로 분해되는 r(s, a) = r_1(o^1, a^1) + r_2(o^2, a^2)를 고려한다. agent가 자신의 goal를 관찰하지만 반드시 팀원의 goal은 관찰하지 않는 game의 경우가 이에 해당한다.
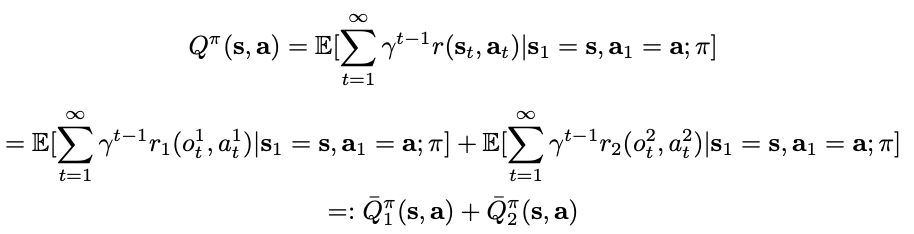
- agent 1's expected future return인 action value function -Q^pi_1(s,a)는 agent 2로 인한 것보다 agent 1으로 인한 (o^1, a^1)에 의해 더 강하게 의존될 것으로 예상할 수 있다.
- 위 Q-function을 (o^1, a^1)으로 모델링하기 어렵다면 agent 1은 LSTM의 historical observation이나 communication channel을 통한 agent 2로부터의 정보를 수신하여 사용할 수 있다. 따라 아래와 같이 approximate가 가능하다.
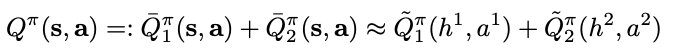
- 우리의 architecture는 이러한 분해를 좀 더 간단한 function으로 만든다. 만약 학습 가능한 parameter 수를 줄이고 싶다면, agent 간의 특정 network weight를 공유할 수 있다. parameter sharing은 agent invariance를 발생시키며 이는 lazy agent problem를 피하는데 유용하다.
VDN results
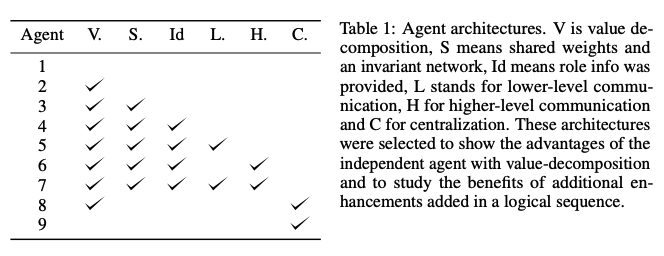
- 실험에서 사용된 V: value decomposition, S: shared weights, L: lower-level communication, H: higher-level communication, C: centralization에 해당되는 agent's options이다.
- Model performance 판단 기준인 ROC의 면적을 의미하는 AUC(Area Under the ROC Curve)를 보면 여러 env에서 비교한 결과 value-decomposition architecture이 individual learner과 centralization보다 훨씬 좋은 성능을 발휘했다.



→ 결과적으로 value decomposition은 fullly centralized 혹은 fully independent 학습자보다 더 나은 성능을 발휘한다.
Conclusion
: Agent에게 single joint reward만 제공하는 cooperative multi-agent RL를 연구한다. 직접 학습하는 individual agent와 fully centralized agent에서의 불만족스러운 결과에 비해 value-decomposition network는 동일한 문제를 겪지 않고 더 좋은 성능을 보여준다. value-decomposotion network는 복잡한 학습 problem을 더 쉽게 학습 가능한 local problem으로 분해하는 단계로 복잡한 task에서 성능을 발휘한다.
→ 그러나 global reward에 영향을 미치는 모든 agents' state / action을 알아야 joint Q-function 학습과 분해가 가능하므로, partial observability 혹은 agent 수가 너무 많아 scalability가 큰 경우엔 실용적이지 않을 수 있을 것 같다.
https://velog.io/@doohyun/QMIX
QMIX
state 가 hypernetwork 지나는 이유Q1 ~ Qn 에 대해 monotonic 하게 Q_tot 가 비례하는 것은 맞으므로 W 원소들이 양수인 것은 맞지만 state가 이 과정에 관여하는 과정에서는 monotonic 할 필요는 없으므로 hyperpa
velog.io
https://koreascience.kr/article/CFKO202125036183305.pdf
댓글