Neural Network(인공신경망)이란?
: 인간 뉴런의 자극 전달 과정에 아이디어를 착안하여 발생한 Machine Learning Algorithm
인간의 뉴런은 시냅스를 통하여 다른 뉴런으로부터 자극을 전달받고 시냅스를 통하여 다른 뉴런에게 자극을 전달하는 과정을 통해서 학습을 진행한다.
이 자극 전달의 과정을 알고리즘 내에서 layer와 perceptron으로 뉴런과 시냅스를 구성하여 연결지은 것이 바로 인공신경망 모형이다. 하나의 뉴런은 곧 하나의 perceptron으로 대응되며, 여러개의 퍼셉트론의 합을 전달해주는 시냅스의 역할은 여러 layer를 잇는 weight/bias(error)가 된다.

위 그림에서 A는 인간의 뉴런을 형상화 한 것이다. 그리고 C는 이 뉴런들의 연결을 보여주는 것이다. B그림을 보면 X1~Xn의 데이터가 들어가서 f(x) = Yi 하나를 출력하는 하나의 퍼셉트론의 형태이고 D는 여러 퍼셉트론을 여러층에 걸쳐서 연결시킨 Multi Layer Perceptron을 나타낸 것이다. 이제부터 이러한 Neural Network의 구조에 대해 자세하게 알아보자.
기본적인 Artificial Neural Network(ANN)의 구조를 알아보면, 입력층(input layer), 은닉층(hidden layer), 출력층(output layer)로 구성되어 있고 각 층은 n개의 노드들로 구성되어 있습니다.

- Input layer(입력층): 예측값(출력 변수)를 도출하기 위한 예측변수(입력변수)의 값들을 입력하는 역할로 만약 n개의 입력값이 있다면 n개의 노드를 보유
- Hidden layer(은닉층): 모든 입력 노드들로부터 입력값을 받아 가중합을 계산하고, 이 값을 전이 함수에 적용하여 출력층에 전달. 각 입력 노드와 은닉 노드, 출력 노드들은 모두 가중치를 가지는 망으로 연결.
- Output layer(출력층): 입력 변수들마다의 가중치로 계산된 예측값 표현 역할
하나의 뉴런에서의 퍼셉트론이 node라고 했을 때, 그 뉴런들을 연결하는 시냅스가 edge인 네트워크를 만드는 것이 가능하다. 이때 각각의 시냅스의 중요도가 다를 수 있으므로 edge마다 weight를 따로 정의하게 되면 다음과 같이 그려진다.

위 그림은 퍼셉트론(Perceptron)을 도식화한 것으로 크게 inputs, weights, transfer function, activation function으로 이루어진다
- input: 입력 데이터이며 n 차원으로 구성
- weight: 가중치의 개수 또한 n 개로 input의 개수와 동일
- transfer function(전이 함수): 이러한 input들의 개별 weight마다 connected 되어 표현된 것으로 선형식의 형태
- weight(가중치): 연결 강도로 표현되며 랜덤으로 초기에 설정되었다가 예측 값을 가장 잘 맞추는 값으로 조정
- activation function(활성함수): 뉴런에 여러 신호가 들어오면 다음 뉴런에 보낼 신호의 강도를 결정하게 되는데, 이때 전달하는 신호의 세기를 정하는 방법. thershhold를 기준으로 특정 집단 구분되며 이것이 하나의 퍼셉트론에서 output으로 도출된다. 추가로 비선형 함수를 사용하게 되며, 전이 함수를 통해 예측값이 전달되기 때문에 NN이 비선형 모델로서 역할이 가능
이러한 퍼셉트론이 여러개 존재할 경우 한 퍼셉트론의 출력값이 다른 퍼셉트론의 입력값이 되며 가중치를 학습하는 과정을 반복한다. 간단한 목차로 나누어 본다면
1. 모든 parameter가 결정되었다고 가정하고 NN이 동작하는 방식 주어진 input에 대해 다음 layer의 activation을 결정 2. 이를 사용하여 그 다음 layer의 activation을 결정
3. 맨 마지막 까지 결정하고 나서 마지막 decision layer의 결과를 보고 inference를 결정(back propagation)
여기서 transfer function은 왜 선형적이여야하고, activaition function은 왜 비선형적이여야 할까?
- 선형 함수: 출력이 입력의 상수배만큼 변하는 함수, 그래프가 직선이다. 프로그래밍적으로 반복문만 사용
- 비선형 함수: 출력이 입력의 상수배가 아닌 함수, 그래프가 직선이 아니다. 프로그래밍적으로 조건문을 사용
만약 f(x) = Wx라는 선형 함수를 activation function으로 지정했다고 가정하고, 3개의 은닉층을 추가로 통과하였다고 할 때, y(x) = f(f(f(x)))이고 이는 식으로 W*W*W*x이다. 이는 W^3=k로 정의해 버리면 y(x) = kx로 표현이 가능하다. 즉, 선형함수로는 은닉층을 여러번 추가하더라도 1회 추가한 것과 차이를 줄 수 없게 된다. 그래서 non-linear activation function을 주로 사용한다.
그러나 선형 함수를 1회 추가한 것과 연속으로 추가한 것이 차이가 없다는 뜻이지, 선형 함수를 사용한 층이 아무 의미도 가지지 못한다는 뜻은 아니다. 학습 가능한 가중치가 새로 생긴다는 점에서 의미가 있다. 이와 같이 선형 함수를 사용한 층을 활성화 함수를 사용하는 은닉층과 구분하기 위해서 선형층(linear layer)이나 투사층(projection layer) 등의 다른 표현을 사용하여 표현하기도 한다. 활성화 함수를 사용하는 일반적인 은닉층을 선형층과 대비되는 표현을 사용하면 비선형층(nonlinear layer)이다.
보통의 ANN는 directed graph(information propagation이 한 방향으로 고정)으로 같은 layer 내에서 서로 connection이 없고(self-loop/parallel edge가 없음) 서로 인접한 layer끼리만 edge를 가진다. 이러한 케이스를 Multi Layer Perceptron(MLP) 구조라고 부르며 information propagation이 'forward'로만 이루어지기 때문에 이런 네트워크를 feed-forward network라고도 칭한다.
만약 undirected edge/ 동일한 directed edge가 양방향으로 주어질 경우 information propagation이 recursive하게 일어나서 결과가 복잡해지는데 이런 경우는 Recurrent NN(RNN)이라 부르고 최근 음성 인식 등의 sequencial data를 처리할 때 쓰이는 등 연구가 활발해지고 있다.
먼저 activation function을 정의해보자. 실제 뇌에서 각기 다른 뉴런이 activate되고 전달되는 과정을 수학적 모델로 바꿔서 생각해보면 input 데이터들에 대한 activation 조건을 function으로 표현하는 것이 가능하다. 사용자가 설정하기 나름이지만 일반적으로 사용되는 activation function이 존재한다.
- Step function(계단 함수)
: 0보다 큰 값이면 1을 반환하고 그렇지 않으면 0을 반환하는 직관적인 함수이다. 그러나 forward 추후에 back propagation시에 gradient 계산이 필요했으므로 미분이 불가능한 형태인 이 모델은 사용이 불가능했다.
import numpy as np
import matplotlib.pyplot as plt
'''
def step_function(x): # 1차원 벡터 비선형 계단 함수
if x > 0:
return 1
else:
return 0
print(step_function(3)) # 0보다 큰 값이면 1을 반환
print(step_function(-0.5)) # 그렇지 않으면 0을 반환
'''
def step_function(x): # numpy tensor 지원 계단 함수
return np.array(x>0, dtype=np.int) # int형 변환
x = np.array([-0.1, 1.0, 2.0])
y = step_function(x)
print(y)
x = np.arange(-5.0, 5.0, 0.1)
y = step_function(x)
plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('step_function(x)')
plt.ylim(-0.1, 1.1)
plt.show()

- Sigmoid fucntion
: 값을 0~1사이의 연속된 값으로 normalize해준다. 과거에 주로 사용되었다.
- Saturation(포화 상태)
: 기울기가 0에 가까워지는 Saturated(Vanishing gradient) 문제 발생
2, 3단 레이어는 학습이 잘 되나 9, 10단을 넘어가면서 부터는 학습이 제대로 이루어 지지 않는다. 레이어가 많을 경우 각각의 단계의 값을 미분해서 최초 레이어까지 결과 값을 전달해 나가게 되는데, 만약 내부의 hidden layer들이 모두 sigmoid함수로 이루어져 있다면 각 단계에서 계산한 값은 모두 0과 1사이의 값일 수밖에 없다.
따라서 여러 layer 보유시, 최초 입력 값은 각각의 layer에서 나온 값들을 곱해준 결과에 영향을 주는 것이므로 최종 미분값은 결국 0에 가까운 값이 될 수밖에 없기 때문에 최초 입력값이 최종 결과값에 별로 영향을 끼치지 않는 결론으로 수렴한다.
- ouputs are not zero-centered(함수값 중심이 0이 아니다)
: input x의 값이 항상 양수라면 gradient W가 항상 양수이거나 항상 음수이기 때문에, 항상 같은 방향으로 움직이게 되는 편향을 보이게 된다.
모든 x 값들이 같은 부호라고 가정하면 한 노드에 대해 모든 파라미터 w의 미분값은 모두 같은 부호를 가지게 된다. 따라서 같은 방향으로 update되는데 이러한 학습을 zigzag 형태로 만들어 느리게 만드는 원인이 된다.
만약 2차원의 W가 존재한다고 가정하고 최적의 해가 w1이 존재했을 때 w2가 감소하는 방향이라면 'zigzag'형태의 비효율적인 weight update가 일어나므로 우리는 일반적으로 zero-mean data를 원한다. input x가 양/음수를 모두 가지고 있으면 w가 전부 양/음수로 움직이는 것을 가능하게 한다.
결국 sigmoid 함수는 vanishing gradien와 not zero-centered 문제 때문에 후에 개선안으로 ReLU 함수를 적용한다.
import numpy as np
import matplotlib.pyplot as plt
def sigmoid(x):
return 1 / (1 +np.exp(-x))
x = np.array([-1.0, 1.0, 2.0])
print(sigmoid(x))
x=np.arange(-5.0, 5.0, 0.5) # -5.0부터 5.0까지 0.5 간격으로 나타낸 값
print(sigmoid(x))
x = np.arange(-5.0, 5.0, 0.1)
y = sigmoid(x)
plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('sigmoid(x)')
plt.ylim(-0.1, 1.1)
plt.show()
- Tanh function(hyperbolic tangent)
: sigmoid를 보완하기 위해 나온 함수로 출력 값은 -1에서 1로 normalization(sigmoid 함수를 재활용하기 위한 함수) sigmoid 보다 성능이 좋다.
- zero-centered
: 중심값을 0으로 옮겨 sigmoid의 최적화 과정이 느려지는 문제를 해결
- still Saturation
: 일정값 이상 커질 시에 여전히 vanishing gradient 존재
import numpy as np
import matplotlib.pylab as plt
x = np.array([-1.0, 1.0, 2.0])
print(np.tanh(x))
x=np.arange(-5.0, 5.0, 0.5) # -5.0부터 5.0까지 0.5 간격으로 나타낸 값
print(np.tanh(x))
# x = np.linspace(-np.pi, np.pi, 201)
x = np.linspace(-5, 5, 1000) # -5.0부터 5.0까지 1000개의 숫자로 나타낸 값
plt.plot(x, np.tanh(x))
plt.xlabel('x')
plt.ylabel('tanh(x)')
plt.ylim(-1.1, 1.1)
plt.show()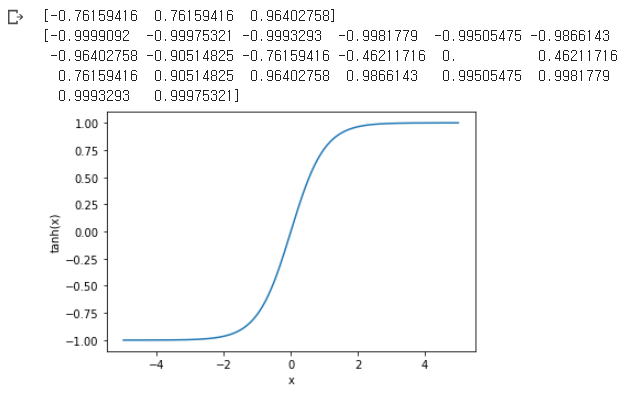
- ReLU function
: 0보다 작은 값이 나온 경우 0을 반환하고 0보다 큰 값이 나온 경우 그 값을 그대로 반환하는 함수
- not Saturated at positive value
- 계산 효율이 뛰어나다. sigmoid/tanh보다 6배정도 빠르다.
- not zero-centered
- Saturated at negative value(dead ReLU)
따라서 내부 hidden layer에는 ReLU를 적용하고 마지막 output layer에서만 sigmoid함수를 적용하면 이전에 비해 정확도가 훨씬 올라가게 된다.

- 초기화를 잘못한 경우
: 가중치 평면이 data cloud에서 멀리 떨어진 경우 어떤 입력 데이터에 대해서 activate되지 않는다.
- learning rate가 너무 높은 경우
: ReLU가 데이터의 영역을 벗어나게 되어 학습이 잘 되던 도중 죽어버리게 된다.
dead ReLU를 피하기 위해 실제 ReLU를 초기화할때 positive biases를 추가하여 weight update시 active ReLU가 될 가능성을 조금이라도 늘려주는 방법이 있다.
import numpy as np
import matplotlib.pyplot as plt
def relu(x) :
return np.maximum(0, x)
x = np.array([-1.0, 1.0, 2.0])
print(relu(x))
x=np.arange(-5.0, 5.0, 0.5) # -5.0부터 5.0까지 0.5 간격으로 나타낸 값
print(relu(x))
x = np.arange(-5.0,5.0,0.1)
plt.plot(x, relu(x))
plt.xlabel('x')
plt.ylabel('ReLU(x)')
plt.ylim(-0.1, 5.1)
plt.show()

- Leakly ReLU function
: Dead ReLU를 해결하기 위해 0에서의 기울기 조정, 음수의 x 값에 대해 미분값이 0이 되지 않는다는 점만 ReLU와 차이점이 존재한다는 특징. 0보다 작은 경우, 0에 근접하는 매우 작은 값으로 변환 되도록 한다. ReLU에 비해 계산 복잡성은 더 크다.
- not Saturated
: ReLU와 유사하지만 음의 영역에서 기울기가 0이 아님
- 여전히 계산이 효율적이며 빠르다.
- no more dead ReLU
import numpy as np
import matplotlib.pyplot as plt
def Leaky_relu(x) :
return np.maximum(0.01*x, x)
x = np.array([-1.0, 1.0, 2.0])
print(Leaky_relu(x))
x=np.arange(-5.0, 5.0, 0.5) # -5.0부터 5.0까지 0.5 간격으로 나타낸 값
print(Leaky_relu(x))
x = np.arange(-5.0,5.0,0.1)
plt.plot(x, Leaky_relu(x))
plt.xlabel('x')
plt.ylabel('Leaky_ReLU(x)')
plt.ylim(-1.1, 5.1)
plt.show()

- PReLU function
: Leakly ReLU와 거의 유사하지만 새로운 파라미터 a를 추가하여 x < 0 에서 기울기 학습 가능, a를 정해놓는 것이 아니라 backpropagation으로 학습시키는 파라미터가 존재하는 특징
- 출력값이 거의 zero-centered에 가까움
import numpy as np
import matplotlib.pyplot as plt
alp = 0.05 # 원래는 설정하면 안되고 backpropagation을 통해 자동 학습. 결과값을 위해 임의 설정
# 추후에 backpropagation 추가하여 구현할 예정
def PReLU(x) :
return np.maximum(alp*x, x)
x = np.array([-1.0, 1.0, 2.0])
print(PReLU(x))
x=np.arange(-5.0, 5.0, 0.5) # -5.0부터 5.0까지 0.5 간격으로 나타낸 값
print(PReLU(x)) # 0에 가까운 값에서 1에 가까운 값으로 커짐
x = np.arange(-5.0,5.0,0.1)
plt.plot(x, PReLU(x))
plt.xlabel('x')
plt.ylabel('PReLU(x)')
plt.ylim(-1.1, 5.1)
plt.show()
- ELU
: ReLU와 유사하지만 0보다 작은 경우에 alpha 값을 이용해서 그래프를 부드럽게 만든다. 따라, elu를 미분해도 부드럽게 이어진다.
import numpy as np
import matplotlib.pyplot as plt
alp = 0.5 # 임의의 alpha 값
def elu(x, alp) :
return (x>0)*x + (x<=0)*(alp*(np.exp(x)-1))
x = np.array([-1.0, 1.0, 2.0])
print(elu(x, alp))
x=np.arange(-5.0, 5.0, 0.5) # -5.0부터 5.0까지 0.5 간격으로 나타낸 값
print(elu(x, alp))
x = np.arange(-5.0,5.0,0.1)
plt.plot(x, elu(x, alp))
plt.xlabel('x')
plt.ylabel('elu(x, alp)')
plt.ylim(-1.1, 5.1)
plt.show()
- Softmax function
: 은닉층에서 ReLU(또는 ReLU 변형) 함수들을 사용하는 것이 일반적이지만 그렇다고 해서 앞서 배운 sigmoid 함수나 softmax 함수가 사용되지 않는다는 의미는 아니다. 분류 문제를 로지스틱 회귀와 소프트맥스 회귀를 출력층(Output layer)에 적용하여 사용한다.
import numpy as np
import matplotlib.pyplot as plt
def softmax(x):
return np.exp(x) / np.sum(np.exp(x))
x = np.array([-1.0, 1.0, 2.0])
print(softmax(x))
x=np.arange(-5.0, 5.0, 0.5) # -5.0부터 5.0까지 0.5 간격으로 나타낸 값
print(softmax(x))
x = np.arange(-5.0,5.0,0.1)
y = np.exp(x) / np.sum(np.exp(x))
plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('softmax(x)')
# plt.ylim(-0.1, 0.1)
plt.show()
여러 활성화 함수들이 존재하고 어떤 함수를 사용해야 하는지에 대한 고찰이 필요하다.
- 가장 많이 사용되는 함수는 ReLU로 갇단하고 사용이 쉽기 때문에 우선적으로 ReLU를 사용한다.
- ReLU를 사용한 이후 Leakly ReLU나 ReLU 계열의 다른 함수도 사용해본다.
- sigmoid는 구시대적 함수이므로 사용하지 않는다.
- tanh의 경우도 큰 성능은 나오지 않는다.
'논문 리뷰 > Neural Network' 카테고리의 다른 글
| RNN, LSTM (0) | 2021.05.06 |
|---|---|
| Multivariable Linear Regression + nn.Module (0) | 2021.03.02 |
| Simple Linear Regression + Cost func / GD (0) | 2021.03.02 |



댓글