Sequence Problem
기존의 NN는 이전에 일어난 사건을 바탕으로 나중에 일어나는 사건에 대해 예측하지 못한다. 은닉층(hidden layer)에서 활성화 함수를 지난 값은 무조건적으로 출력층(output layer) 방향으로 향하는 Feed-Forward의 특징을 지닌다. 이와 다르게 RNN은 은닉층의 노드에서 활성화 함수를 통해 나온 결과값을 출력층 방향으로 보내면서, 다시 은닉층 노드의 다음 계산의 입력으로 보내는 특징을 가진다. 스스로를 반복하면서 이전 단계에서 얻은 정보가 지속되도록 하는 구조의 체인처럼 이어지는 성질은 Sequence나 list로 이어지는 것을 알려준다. 즉, RNN은 Sequence data Problem를 다루기에 최적화된 구조의 NN이라고 생각할 수 있다. 그리고 입력과 출력이 일련의 시퀀스(Sequence)로 구성되는 데이터가 사용되는 음성인식, 언어 모델링, 번역, 이미지 주석 생성과 같은 다양한 분야에서 굉장한 성공을 이루었다.
Recurrent Neural Network
RNN에서 은닉층에서 활성화 함수를 통해 결과를 내보내는 역할을 하는 노드를 셀(cell)이라고 한다. 이 셀은 이전의 값을 기억하려고 하는 일종의 메모리 역할을 수행하므로 이를 메모리 셀 또는 RNN 셀이라고 표현된다. 은닉층의 메모리 셀은 각각의 시점(time step)에서 바로 이전 시점에서의 은닉층의 메모리 셀에서 나온 값을 자신의 입력으로 사용하는 재귀적 활동을 하고 있다.
현재 시점을 t라고 표현했을 때, 현재 시점 t에서의 메모리 셀이 갖고있는 값은 과거의 메모리 셀들의 값에 영향을 받은 것임을 의미하고, 은닉상태(hidden state)라고 한다. 다시 말해 t 시점의 메모리 셀은 t-1 시점의 메모리 셀이 보낸 은닉 상태값을 t 시점의 은닉 상태 계산을 위한 입력값으로 사용한다.
Xt: 입력층의 입력 벡터, Ht: 출력층의 출력 벡터, A: RNN 셀 / 메모리 셀
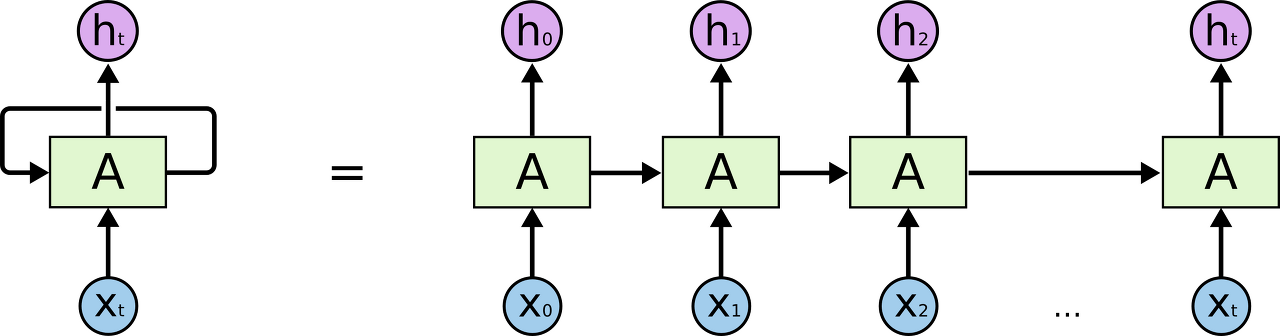
RNN Basic
RNN 코드를 살펴보기에 앞서 구조 이해를 위해 크게 두가지로 분리한다. 다음과 같이 나누어 구성하게 되면 이식성이 높아, 효과적인 학습을 위해서 원하는 cell 혹은 data 값들을 바꾸기만 하면 수정이 된다.
1. cell 생성
: num_units = hidden_size이며 출력값인 Ht의 크기를 정한다.
cell = tf.contrib.rnn.BasicRNNCell(num_units=hidden_size)
cell = tf.contrib.rnn.BasicLSTMCell(num_units=hidden_size)
2. 만든 cell을 통해 어떤 학습을 하고 구동하는지 결정
: 위에서 생성한 cell과 x_data를 넘겨주면 outputs, _states 값을 반환한다.
outputs, _states = tf.nn.dynamic_rnn(cell, x_data, dtype=tf.float32)
setting input dimension, output dimension
: 입력을 one-hot encoding으로 x_data = [1, 0, 0, 0]를 4d로 전처리하고, 출력을 hidden size = 2를 2d로 사용자의 설정값으로 표현했다. 입력 dimension은 사용자가 전처리하기 나름이고, 출력 dimension 또한 사용자가 설정 가능하다.
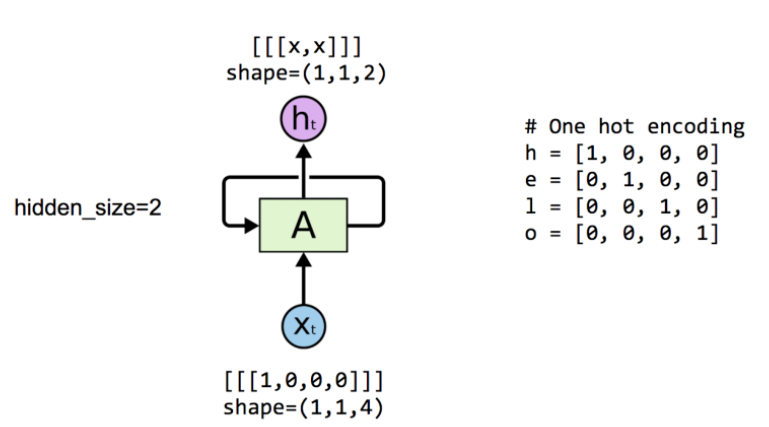
# cell 생성 시 hidden_size를 2로 설정해 출력값이 2가지로 나오도록 설정
hidden_size = 2
cell = tf.contrib.rnn.BasicLSTMCell(num_units=hidden_size)
# 4개의 vector가 있는 data하나 생성
x_data = np.array([[[1,0,0,0]]], dtype=np.float32)
# cell과 입력 데이터를 직접 넘김 -> output,_states 생성
outputs, _states = tf.nn.dynamic_rnn(cell, x_data, dtype=tf.float32)
# value_initialize한 뒤, 세션을 실행
sess.run(tf.global_variables_initializer())
# output를 evaluation하는 방식으로 출력
pp.pprint(outputs.eval())
-> array([[[-0.42409304, 0.64651132]]])
setting sequence length
: 위와 동일한 입출력 dimension 상태에서, 시퀀스 데이터 몇개를 받을 것인가에 대한 sequence_length 설정은 입력 데이터를 줄 때 모양(길이)에 따라 결정된다. 사용자가 직접 지정하는 것이 아니다.
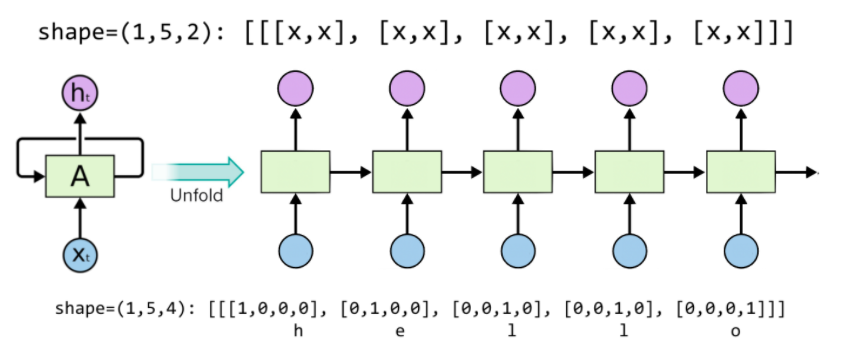
각각의 데이터 h, e, l, o를 변수로 선언하여 4d vector로 one-hot encoding한 것이 5개의 시퀀스로 연결되어 있다.
# One-hot encoding
h = [1, 0, 0, 0]
e = [0, 1, 0, 0]
l = [0, 0, 1, 0]
o = [0, 0, 0, 1]
hidden_size = 2
cell = tf.contrib.rnn.BasicLSTMCell(num_units=hidden_size)
# Sequence_length를 5로 하여 x_data 설정
x_data = np.array([[h, e, l, l, o]], dtype=np.float32)
print(x_data.shape)
-> 1, 5, 4
pp.pprint(x_data)
-> x_data = array
([[[ 1., 0., 0., 0.],
[ 0., 1., 0., 0.],
[ 0., 0., 1., 0.],
[ 0., 0., 1., 0.],
[ 0., 0., 0., 1.]]], dtype=float32)
outputs, states = tf.nn.dynamic_rnn(cell, x_data, dtype=tf.float32)
sess.run(tf.global_variables_initializer())
print(x_data.shape)
-> 1, 5, 2
pp.pprint(outputs.eval())
-> outputs = array # RNN 속 초기화된 weight들
([[[ 0.19709368, 0.24918222],
[-0.11721198, 0.1784237 ],
[-0.35297349, -0.66278851],
[-0.70915914, -0.58334434],
[-0.38886023, 0.47304463]]], dtype=float32) # dimension 2개 * 5
setting batch size
: 학습 시, 문자열 한 줄씩 학습하는 것은 비효율적이기 때문에 batch_size를 통해 데이터 여러개를 동시에 학습하기 위해 입력 데이터를 아래와 같이 제공한다.
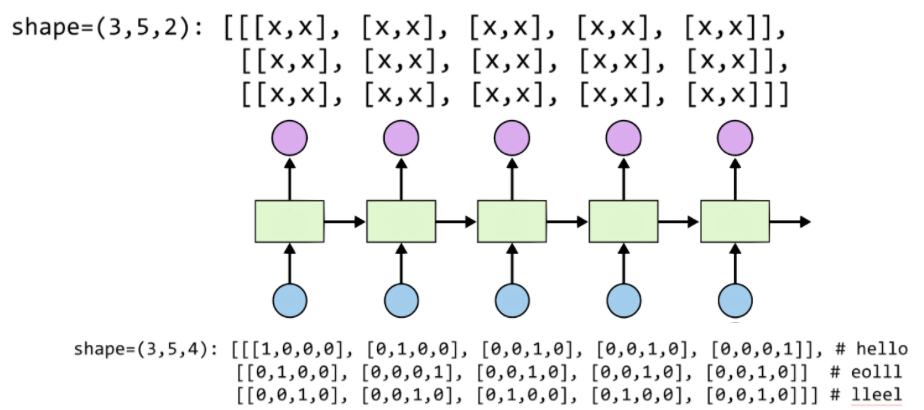
# 3 batches 'hello', 'eolll', 'lleel'
x_data = np.array([[h, e, l, l, o],
[e, o, l, l, l],
[l, l, e, e, l]], dtype=np.float32)
pp.pprint(x_data)
-> x_data= array([[[ 1., 0., 0., 0.],
[ 0., 1., 0., 0.],
[ 0., 0., 1., 0.],
[ 0., 0., 1., 0.],
[ 0., 0., 0., 1.]],
[[ 0., 1., 0., 0.],
[ 0., 0., 0., 1.],
[ 0., 0., 1., 0.],
[ 0., 0., 1., 0.],
[ 0., 0., 1., 0.]],
[[ 0., 0., 1., 0.],
[ 0., 0., 1., 0.],
[ 0., 1., 0., 0.],
[ 0., 1., 0., 0.],
[ 0., 0., 1., 0.]]],
cell = rnn.BasicLSTMCell(num_units=2, state_is_tuple=True)
outputs, _states = tf.nn.dynamic_rnn(cell, x_data, dtype=tf.float32)
sess.run(tf.global_variables_initializer())
pp.pprint(outputs.eval())
-> outputs = array([[[-0.0173022 , -0.12929453],
[-0.14995177, -0.23189341],
[ 0.03294011, 0.01962204],
[ 0.12852104, 0.12375218],
[ 0.13597946, 0.31746736]],
[[-0.15243632, -0.14177315],
[ 0.04586344, 0.12249056],
[ 0.14292534, 0.15872268],
[ 0.18998367, 0.21004884],
[ 0.21788891, 0.24151592]],
[[ 0.10713603, 0.11001928],
[ 0.17076059, 0.1799853 ],
[-0.03531617, 0.08993293],
[-0.1881337 , -0.08296411],
[-0.00404597, 0.07156041]]],
Teach RNN 'hihello'
: 내가 특정 문자를 주면 그 다음문자를 예측하는 모델을 구현한다. h가 두개여서 어느 시퀀스에서의 h인지 판단하기 위해 이전 값들에 대한 데이터 또한 필요하기에 RNN으로 구현해야 한다.
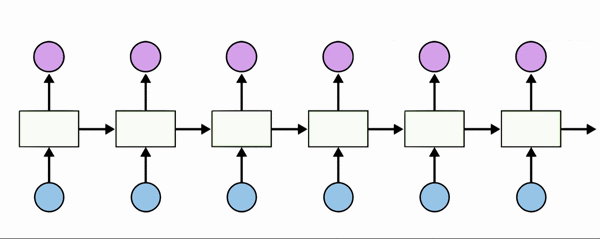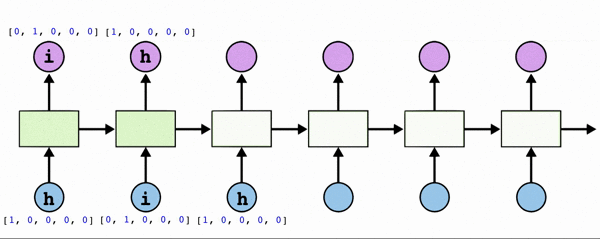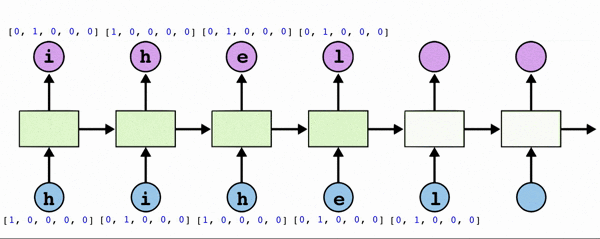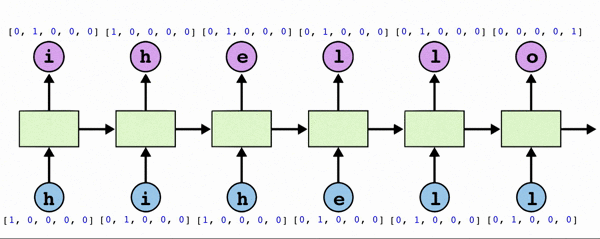
- text: ‘hihello'
- unique chars(vocabulary, voc): h, i, e, l, o
- voc index: h:0, i:1, e:2, l:3, o:4
# One-hot encoding으로 다음과 같이 문자를 표현
[1, 0, 0, 0, 0], # h 0
[0, 1, 0, 0, 0], # i 1
[0, 0, 1, 0, 0], # e 2
[0, 0, 0, 1, 0], # l 3
[0, 0, 0, 0, 1], # o 4
# 자연스럽게 목적 변수들 설정이 가능
input dimension = 5
output dimension = 5(hidden)
sequence_length = 6
batch_size = 1
# RNN model
# cell 설정은 다음 중 아무거나 넣어줘도 상관 없음, output_dimension = 5이므로 rnn_size = 5
rnn_cell = rnn_cell.BasicRNNCell(rnn_size = 5)
rnn_cell = rnn_cell. BasicLSTMCell(rnn_size = 5)
rnn_cell = rnn_cell. GRUCell(rnn_size = 5)
# model 설정
outputs, _states = tf.nn.dynamic_rnn(rnn_cell, X, # cell이랑 X_data 그대로 넘겨줌
initial_state=initial_state, dtype=tf.float32)
data creation
# index를 char로 만드는 dictionary 기능 수행
idx2char = ['h', 'i', 'e', 'l', 'o'] # h=0, i=1, e=2, l=3, o=4
# input data
x_data = [[0, 1, 0, 2, 3, 3]] # hihell
x_one_hot = [[[1, 0, 0, 0, 0], # h 0
[0, 1, 0, 0, 0], # i 1
[1, 0, 0, 0, 0], # h 0
[0, 0, 1, 0, 0], # e 2
[0, 0, 0, 1, 0], # l 3
[0, 0, 0, 1, 0]]] # l 3
# true data
y_data = [[1, 0, 2, 3, 3, 4]] # ihello
feed to RNN
# 훈련을 위한 tensor화
# X one-hot
X = tf.placeholder(tf.float32, [None = batch_size, sequence_length = 6, input_dimension = 5])
# Y label
Y = tf.placeholder(tf.int32, [None = batch_size, sequence_length = 6])
# cell 생성
cell = tf.contrib.rnn.BasicLSTMCell(num_units=hidden_size= 5, state_is_tuple=True)
# initial hidden state 설정
initial_state = cell.zero_state(batch_size, tf.float32) # batch_size주고 0으로 설정
# rnn 구성
outputs, _states = tf.nn.dynamic_rnn(cell, X, initial_state=initial_state, dtype=tf.float32)
Cost: Sequence_loss
: RNN에서 loss를 계산하기 위한 함수
ver1.
# [batch_size, sequence_length] true data
y_data = tf.constant([[1, 1, 1]])
# [batch_size, sequence_length, emb_dim ] prediction data(sequence로 주어짐)
prediction = tf.constant([[[0.2, 0.7], [0.6, 0.2], [0.2, 0.9]]], dtype=tf.float32)
1 0 1로 prediction
# [batch_size * sequence_length] 자리에 대한 중요도, 모두 같으므로 1
weights = tf.constant([[1, 1, 1]], dtype=tf.float32)
sequence_loss = tf.contrib.seq2seq.sequence_loss(logits=prediction, targets=y_data, weights=weights)
sess.run(tf.global_variables_initializer())
print("Loss: ", sequence_loss.eval())
-> Loss: 0.596759
ver2.
# [batch_size, sequence_length]
y_data = tf.constant([[1, 1, 1]])
# [batch_size, sequence_length, emb_dim ]
prediction1 = tf.constant([[[0.3, 0.7], [0.3, 0.7], [0.3, 0.7]]], dtype=tf.float32) # 약한 예측
prediction2 = tf.constant([[[0.1, 0.9], [0.1, 0.9], [0.1, 0.9]]], dtype=tf.float32) # 강한 예측
1 1 1로 prediction
# [batch_size * sequence_length]
weights = tf.constant([[1, 1, 1]], dtype=tf.float32)
# loss 비교해보자
sequence_loss1 = tf.contrib.seq2seq.sequence_loss(prediction1, y_data, weights)
sequence_loss2 = tf.contrib.seq2seq.sequence_loss(prediction2, y_data, weights)
sess.run(tf.global_variables_initializer())
print("Loss1: ", sequence_loss1.eval(),
"Loss2: ", sequence_loss2.eval())
-> Loss1: 0.513015
Loss2: 0.371101 # 실제와 가까워질수록 loss가 낮아진다.
outputs, _states = tf.nn.dynamic_rnn(cell, X, initial_state=initial_state, dtype=tf.float32)
weights = tf.ones([batch_size, sequence_length])
# 앞에서 배운 sequenc_loss로 계산
sequence_loss = tf.contrib.seq2seq.sequence_loss(logits=outputs, targets=Y, weights=weights)
# loss를 평균
loss = tf.reduce_mean(sequence_loss)
# Adam optimizer로 loss 최소화 학습 진행
train = tf.train.AdamOptimizer(learning_rate=0.1).minimize(loss)
Training
# One-hot에서 나온 max 값을 prediction으로 취함
prediction = tf.argmax(outputs, axis=2)
with tf.Session() as sess: # sesstion 열고
sess.run(tf.global_variables_initializer()) # 초기화 진행
for i in range(2000):
# x_one_hot, y_data 넘겨주며 훈련 진행
l, _ = sess.run([loss, train], feed_dict={X: x_one_hot, Y: y_data}) # rnn run
result = sess.run(prediction, feed_dict={X: x_one_hot}) # prediction
print(i, "loss:", l, "prediction: ", result, "true Y: ", y_data)
# print char using dic: prediction의 숫자를 문자화
result_str = [idx2char[c] for c in np.squeeze(result)]
print("\tPrediction str: ", ''.join(result_str))
-> training
step loss random init prediction y_data char
0 loss: 1.55474 prediction: [[3 3 3 3 4 4]] true Y: [[1, 0, 2, 3, 3, 4]] Prediction str: lllloo
1 loss: 1.55081 prediction: [[3 3 3 3 4 4]] true Y: [[1, 0, 2, 3, 3, 4]] Prediction str: lllloo
2 loss: 1.54704 prediction: [[3 3 3 3 4 4]] true Y: [[1, 0, 2, 3, 3, 4]] Prediction str: lllloo
3 loss: 1.54342 prediction: [[3 3 3 3 4 4]] true Y: [[1, 0, 2, 3, 3, 4]] Prediction str: lllloo
...
1998 loss: 0.75305 prediction: [[1 0 2 3 3 4]] true Y: [[1, 0, 2, 3, 3, 4]] Prediction str: ihello
1999 loss: 0.75297 prediction: [[1 0 2 3 3 4]] true Y: [[1, 0, 2, 3, 3, 4]] Prediction str: ihello
RNN with long Sequences
Manual data creation(before)
idx2char = ['h', 'i', 'e', 'l', 'o']
x_data = [[0, 1, 0, 2, 3, 3]] # hihell
x_one_hot = [[[1, 0, 0, 0, 0], # h 0
[0, 1, 0, 0, 0], # i 1
[1, 0, 0, 0, 0], # h 0
[0, 0, 1, 0, 0], # e 2
[0, 0, 0, 1, 0], # l 3
[0, 0, 0, 1, 0]]] # l 3
y_data = [[1, 0, 2, 3, 3, 4]] # ihello
Better data creation(new) & Hyper parameters
# unique character <-> index 전환 함수
sample = " if you want you"
idx2char = list(set(sample)) # index -> char
char2idx = {c: i for i, c in enumerate(idx2char)} # char -> idx
sample_idx = [char2idx[c] for c in sample] # char to index: sample의 char를 index로 가져옴
x_data = [sample_idx[:-1]] # X data sample (0 ~ n-1) hello: hell
y_data = [sample_idx[1:]] # Y label sample (1 ~ n) hello: ello
X = tf.placeholder(tf.int32, [None, sequence_length]) # X data
Y = tf.placeholder(tf.int32, [None, sequence_length]) # Y label
# X와 num_classes=idx2char(unique char 개수)를 넣어줘서 One-hot encoding 진행
X_one_hot = tf.one_hot(X, num_classes) # one hot: 1 -> 0 1 0 0 0 0 0 0 0 0
# 우리가 가진 데이터들로 hyper parameters 자동 생성
dic_size = len(char2idx) # RNN input size (one hot size)
rnn_hidden_size = len(char2idx) # RNN output size
num_classes = len(char2idx) # final output size (RNN or softmax, etc.)
batch_size = 1 # one sample data, one batch
sequence_length = len(sample) - 1 # number of lstm unfolding (unit #)
LSTM and Loss
X = tf.placeholder(tf.int32, [None, sequence_length]) # X data
Y = tf.placeholder(tf.int32, [None, sequence_length]) # Y label
X_one_hot = tf.one_hot(X, num_classes) # one hot: 1 -> 0 1 0 0 0 0 0 0 0 0
cell = tf.contrib.rnn.BasicLSTMCell(num_units=rnn_hidden_size, state_is_tuple=True)
initial_state = cell.zero_state(batch_size, tf.float32)
outputs, _states = tf.nn.dynamic_rnn(cell, X_one_hot, initial_state=initial_state, dtype=tf.float32)
weights = tf.ones([batch_size, sequence_length])
sequence_loss = tf.contrib.seq2seq.sequence_loss(logits=outputs, targets=Y,weights=weights)
loss = tf.reduce_mean(sequence_loss)
train = tf.train.GradientDescentOptimizer(learning_rate=0.1).minimize(loss)
prediction = tf.argmax(outputs, axis=2)
Training and Results
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for i in range(3000):
l, _ = sess.run([loss, train], feed_dict={X: x_data, Y: y_data})
result = sess.run(prediction, feed_dict={X: x_data})
# print char using dic
result_str = [idx2char[c] for c in np.squeeze(result)]
print(i, "loss:", l, "Prediction:", ''.join(result_str))
->
0 loss: 2.29895 Prediction: nnuffuunnuuuyuy
1 loss: 2.29675 Prediction: nnuffuunnuuuyuy
...
1418 loss: 1.37351 Prediction: if you want you
1419 loss: 1.37331 Prediction: if you want you
RNN with Really long sentence
sentence = ("if you want to build a ship, don't drum up people together to "
"collect wood and don't assign them tasks and work, but rather "
"teach them to long for the endless immensity of the sea.")
# training dataset
0 if you wan -> f you want
1 f you want -> you want
2 you want -> you want t
3 you want t -> ou want to
…
168 of the se -> of the sea
169 of the sea -> f the sea.
Making dataset
# 기존과 똑같이 unique char <-> index
char_set = list(set(sentence))
char_dic = {w: i for i, w in enumerate(char_set)}
dataX = []
dataY = []
# long sentence를 seq_length만큼 잘라서 윈도우를 1씩 이동해 dataX, dataY 생성
for i in range(0, len(sentence) - seq_length):
x_str = sentence[i:i + seq_length]
y_str = sentence[i + 1: i + seq_length + 1]
print(i, x_str, '->', y_str)
#
x = [char_dic[c] for c in x_str] # x str to index
y = [char_dic[c] for c in y_str] # y str to index
dataX.append(x)
dataY.append(y)
RNN parameters & run
char_set = list(set(sentence))
char_dic = {w: i for i, w in enumerate(char_set)}
data_dim = len(char_set)
hidden_size = len(char_set)
num_classes = len(char_set)
seq_length = 10 # Any arbitrary number 임의로 지정
batch_size = len(dataX) # 전체 array를 한번에 입력
X = tf.placeholder(tf.int32, [None, sequence_length]) # X data
Y = tf.placeholder(tf.int32, [None, sequence_length]) # Y label
X_one_hot = tf.one_hot(X, num_classes) # one hot: 1 -> 0 1 0 0 0 0 0 0 0 0
cell = tf.contrib.rnn.BasicLSTMCell(num_units=rnn_hidden_size, state_is_tuple=True)
initial_state = cell.zero_state(batch_size, tf.float32)
outputs, _states = tf.nn.dynamic_rnn(
cell, X_one_hot, initial_state=initial_state, dtype=tf.float32)
weights = tf.ones([batch_size, sequence_length])
sequence_loss = tf.contrib.seq2seq.sequence_loss(logits=outputs, targets=Y,weights=weights)
loss = tf.reduce_mean(sequence_loss)
train = tf.train.GradientDescentOptimizer(learning_rate=0.1).minimize(loss)
prediction = tf.argmax(outputs, axis=2)
Stacked RNN
위 RNN은 원활한 학습이 불가능하다. 이를 해결하기 위해 다음의 방식을 접근해본다.
1. RNN을 multi-layer로 구성
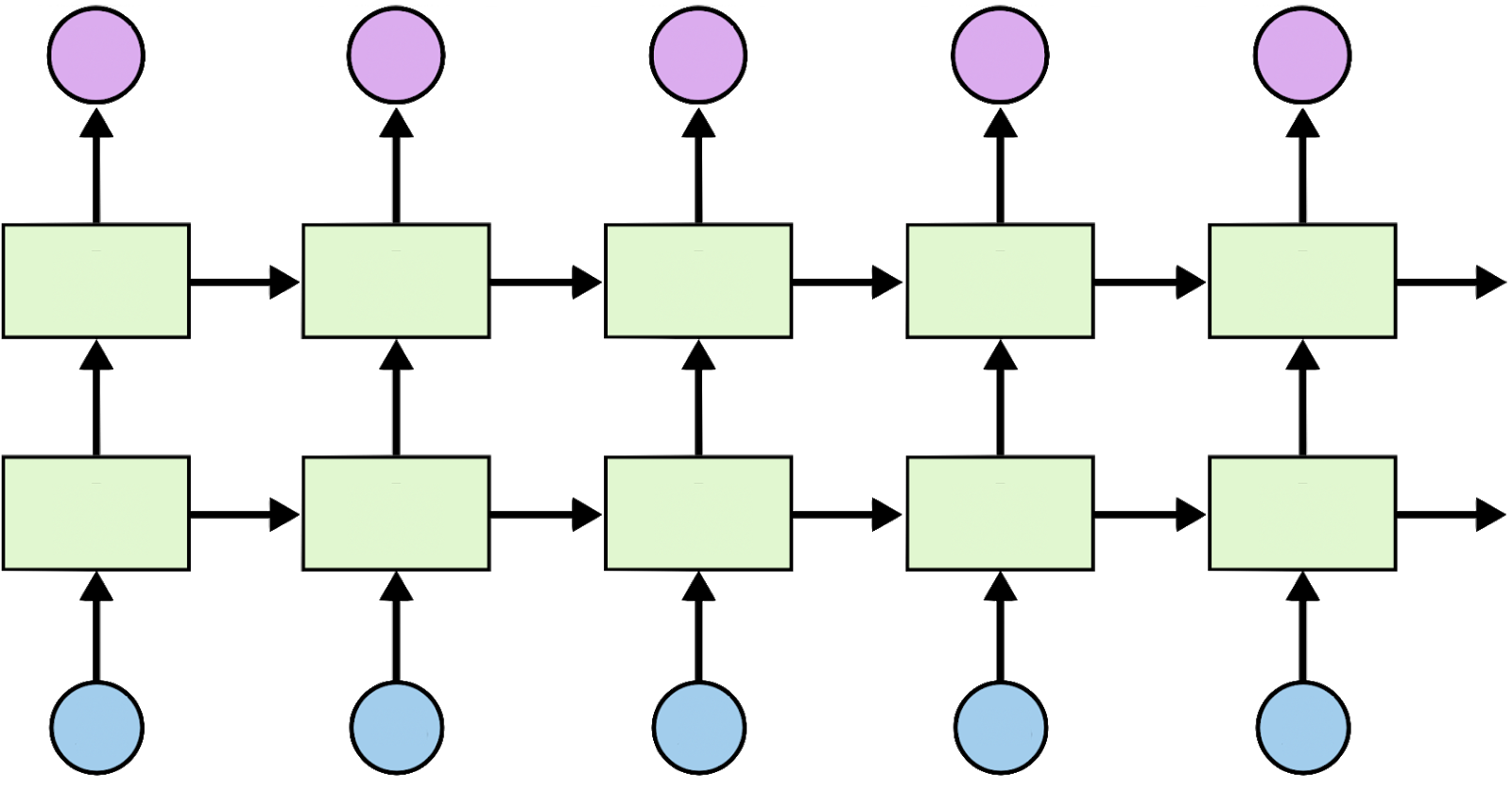
X = tf.placeholder(tf.int32, [None, seq_length])
Y = tf.placeholder(tf.int32, [None, seq_length])
# One-hot encoding
X_one_hot = tf.one_hot(X, num_classes)
print(X_one_hot) # check out the shape
# Make a lstm cell with hidden_size (each unit output vector size)
cell = rnn.BasicLSTMCell(hidden_size, state_is_tuple=True)
cell = rnn.MultiRNNCell([cell] * 2, state_is_tuple=True) # [cell] * n 개의 층을 쌓기 가능
# outputs: unfolding size x hidden size, state = hidden size
outputs, _states = tf.nn.dynamic_rnn(cell, X_one_hot, dtype=tf.float32)
2. RNN에서의 값을 그대로 사용하기보다는 FC layer를 추가
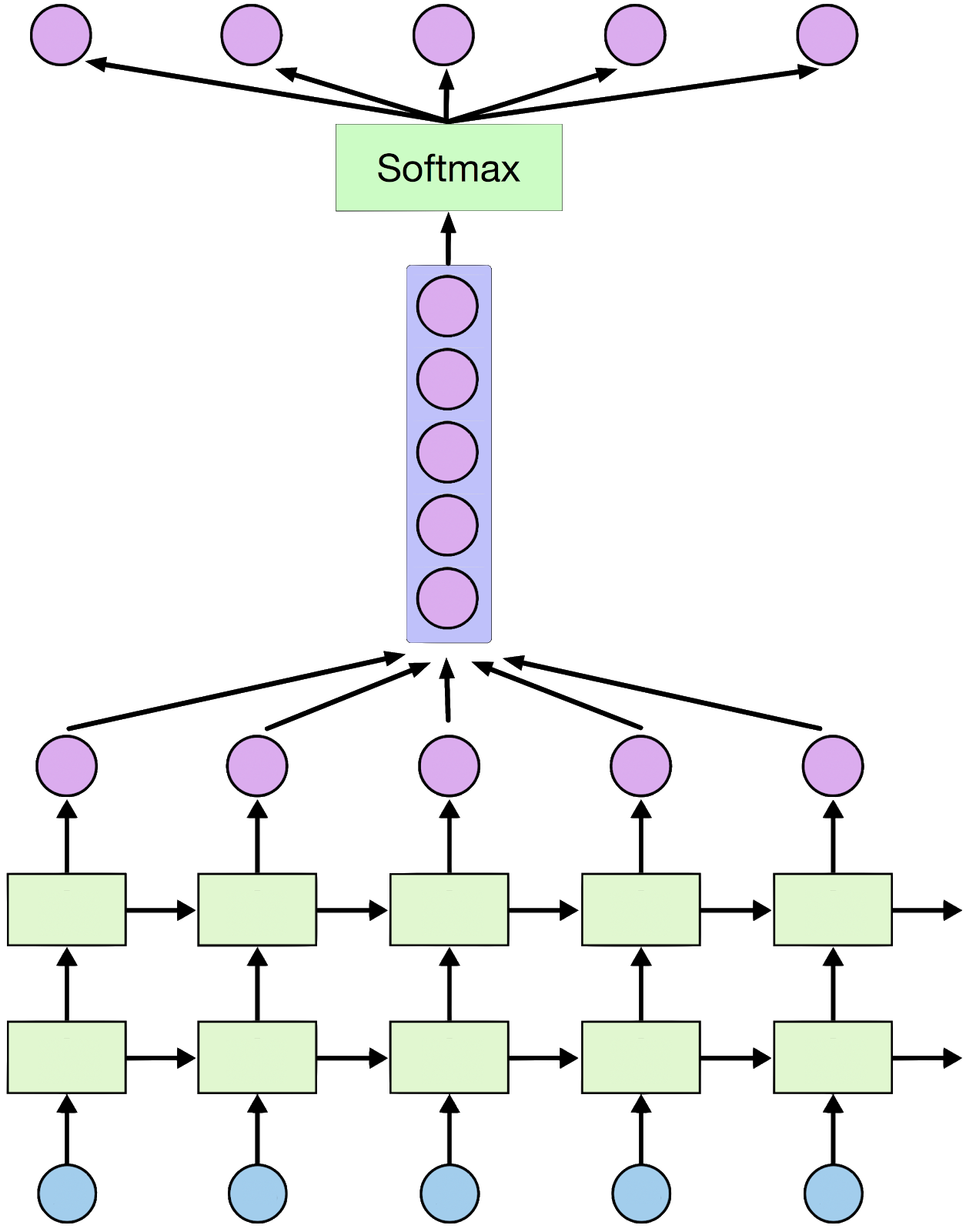
# FC layer를 위한 reshape 과정
# (optional) FC layer를 위한 입력 reshape
X_for_softmax = tf.reshape(outputs, [-1, hidden_size]) # rnn에서 나온 ouputs, [전과 동일, hidden_size]
# weight, bias size 정의
softmax_w = tf.get_variable("softmax_w",
[hidden_size, num_classes] # input, output(실제로는 같은 값)
softmax_b = tf.get_variable("softmax_b",[num_classes]) # output
outputs = tf.matmul(X_for_softmax,softmax_w) + softmax_b # softmax output(activation func 안거침)
# reshape out for sequence_loss
# FC layer에서 나온 output을 펼쳐주는 과정
outputs = tf.reshape(outputs, # rnn의 output shape와 동일
[batch_size, seq_length, num_classes])
# All weights are 1 (equal weights)
weights = tf.ones([batch_size, seq_length])
sequence_loss = tf.contrib.seq2seq.sequence_loss(
# 원래 logit에 activation func를 안거친 FC layer outputs를 넣어주었어야함
logits=outputs, targets=Y, weights=weights)
mean_loss = tf.reduce_mean(sequence_loss)
train_op = tf.train.AdamOptimizer(learning_rate=0.1).minimize(mean_loss)
Training and print results
sess = tf.Session()
sess.run(tf.global_variables_initializer()
for i in range(500):
_, l, results = sess.run([train_op, mean_loss, outputs],
feed_dict={X: dataX, Y: dataY})
# char result로 출력
for j, result in enumerate(results):
index = np.argmax(result, axis=1)
print(i, j, ''.join([char_set[t] for t in index]), l)
->
0 167 tttttttttt 3.23111
0 168 tttttttttt 3.23111
0 169 tttttttttt 3.23111
…
499 167 oof the se 0.229306
499 168 tf the sea 0.229306
499 169 n the sea. 0.229306
# Let's print the last char of each result to check it works
results = sess.run(outputs, feed_dict={X: dataX})
for j, result in enumerate(results):
index = np.argmax(result, axis=1)
if j is 0: # print all for the first result to make a sentence
print(''.join([char_set[t] for t in index]), end='')
else:
print(char_set[index[-1]], end='')
->
0 167 tttttttttt 3.23111
0 168 tttttttttt 3.23111
0 169 tttttttttt 3.23111
…
499 167 of the se 0.229616
499 168 tf the sea 0.229616
499 169 the sea. 0.229616
g you want to build a ship, don't drum up people together to collect wood and don't assign them tasks and work, but rather teach them to long for the endless immensity of the sea.
'''
Dynamic RNN
RNN with time series data
Natural Language Processing(NLP)
앞의 두 단어를 보고, 뒤에 나올 단어를 예측하는 예제
RNN code
RNN problem
RNN은 비교적 short sequence에서만 효과를 보이는 단점이 존재한다. 따라 time step이 길어질 수록 앞의 정보가 뒤로 충분히 전달되지 못하는 현상이 발생하게 된다. 아래의 그림처럼 첫번 째 입력값인 x1의 정보량의 짙음이 time step이 흐를 수록 색이 얕아지고 정보량이 손실되어가는 과정을 의미한다. 뒤로 갈수록 x1의 정보량은 손실되고, long sequence의 경우에는 x1의 전체 정보에 대한 영향력은 의미가 미미해진다. 이를 장기 의존성 문제(problem of Long-Term Dependencies)라고 한다.
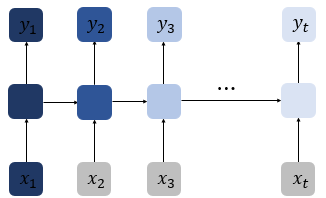
RNN architecture
RNN의 내부를 살펴보자면 NN 모듈을 반복시키는 체인과 같은 형태를 보인다. 기본적인 RNN은 굉장히 단순한 구조로 tanh layer 한층으로 반복된다.
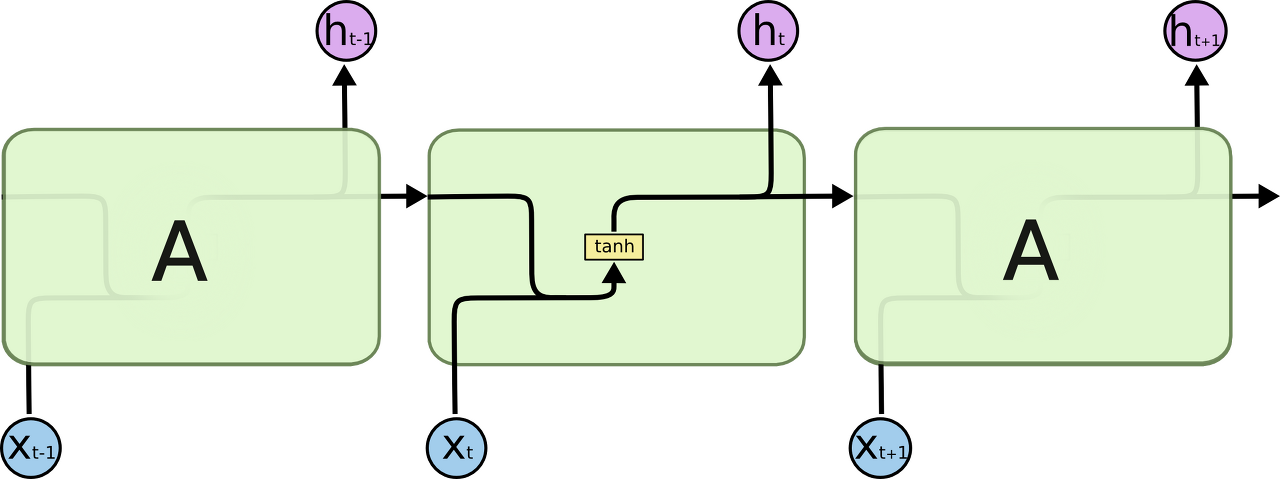
LSTM
RNN의 장기 의존성 문제를 해결하기 위해 만들어진 장단기 메모리(Long Short-Term Memory)이다. 이 또한 RNN의 일종이다. LSTM은 hidden layer의 메모리 셀에 입력 게이트, 망각 게이트, 출력 게이트를 추가하여 불필요한 기억을 지우고, 기억해야할 것들을 정한다. 요약하면 LSTM은 은닉 상태(hidden state)를 계산하는 식이 기존의 RNN보다 조금 더 복잡해졌으며 셀 상태(cell state)라는 값이 추가되었다. LSTM은 RNN과 비교하여 long sequence의 입력을 처리하는데 탁월한 성능을 보인다.
LSTM architecture
LSTM도 똑같이 체인 구조를 가지고 있지만, 반복 모듈은 다른 구조를 지닌다. 위에서 tanh layer 한층 사용 대신 4개의 layer가 특정 방식으로 서로 정보를 주고 받도록 설계되어있다.
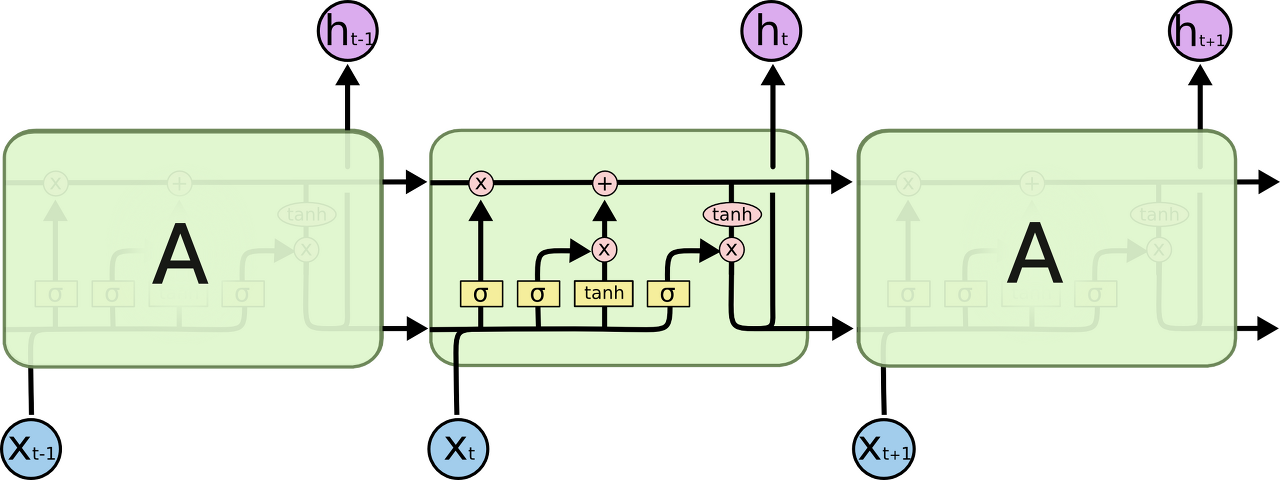
Symbol Definition

- 분홍 동그라미: vector 합과 같은 pointwise opertaion
- 노란색 박스: 학습된 Neural Network layer
- 선: 한 node의 output을 다른 node의 input으로 vector 전체를 보내는 흐름
- 합쳐지는 선: Concatenatation; 결합
- 갈라지는 선: Fork; 복사해서 다른쪽으로 전송
main Idea
Cell state: 모듈 그림에서 수평으로 그어진 윗 선에 해당, 컨베이어 밸트처럼 작은 linear interaction만을 적용시키면서 전체 체인을 계속 구동시킨다. 셀 상태 또한 이전에 배운 은닉 상태처럼 이전 시점의 Cell state가 다음 시점의 Cell state를 구하기 위한 입력으로서 사용된다. LSTM은 cell state에 뭔가를 더하거나 없앨 수 있는 능력이 있는데, 이 능력은 gate라고 불리는 구조에 의해서 조심스럽게 제어된다.
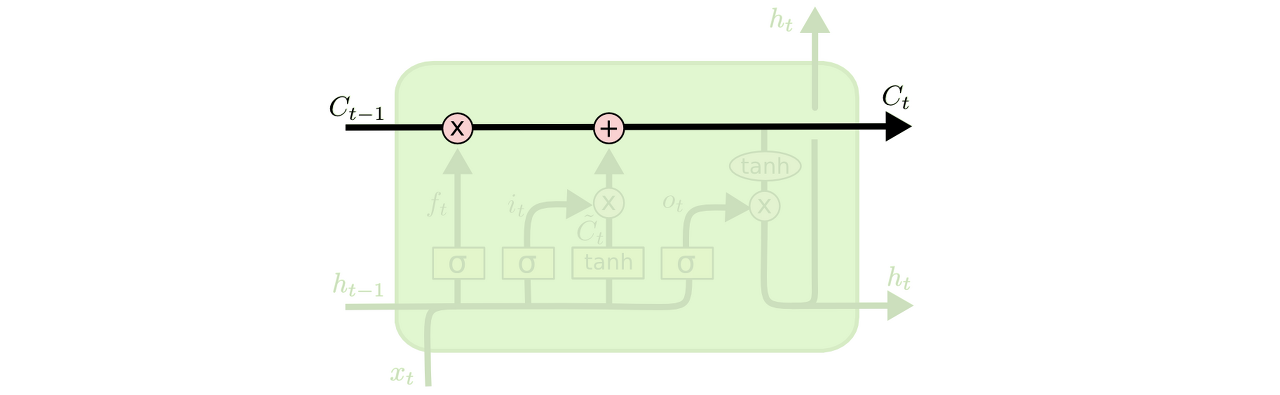
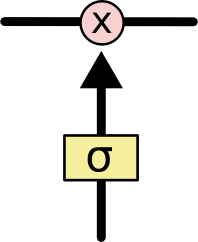
Gate: 정보가 전달될 수 있는 추가적인 방법으로, 모두 Sigmoid layer가 존재하고 이는 0과 1 사이의 숫자를 내보내는데, 이 값은 각 컴포넌트가 얼마나 정보를 전달해야 하는지에 대한 척도를 나타낸다. 그 값이 0이라면 "아무 것도 넘기지 말라"가 되고, 값이 1이라면 "모든 것을 넘겨라"가 된다.
LSTM은 3개의 gate를 가지고 있고, 이 문들은 cell state를 보호하고 제어한다. 각 gate와 input에 따른 가중치들이 존재하며, xt와 함께 게이트에서 사용되는 가중치 4개, ht-1와 함께 게이트에서 사용되는 가중치 4개, 각 게이트에서 사용되는 편향 4개가 존재한다.
LSTM Progress
1. cell state로부터 어떤 정보를 버릴 것인지를 정한다.
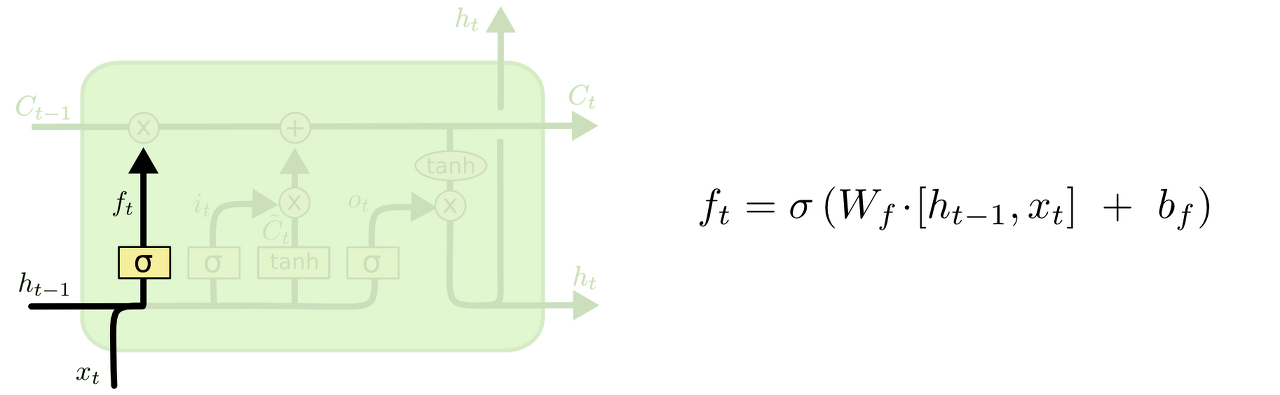
이 gate를 "forget gate layer"라고 부르고, sigmoid layer에 의해 결정된다. 이 단계에서는 과 를 받아서 0과 1 사이의 값을 Ct−1에 보내준다. sigmoid 함수를 지나면 0과 1 사이의 값이 나오게 되는데, 이 값이 곧 삭제 과정을 거친 정보의 양이다. 0에 가까울수록 정보가 많이 삭제된 것이고 1에 가까울수록 정보를 온전히 기억한 것.
이전 단어들을 바탕으로 다음 단어를 예측하는 언어 모델 예시를 들자면
ex) 여기서 cell state는 현재 주어의 성별 정보를 가지고 있을 수도 있어서 그 성별에 맞는 대명사가 사용되도록 준비하고 있을 수도 있을 것이다. 그런데 새로운 주어가 왔을 때, 우리는 기존 주어의 성별 정보를 생각하고 싶지 않을 것이다.
2. 앞으로 들어오는 새로운 정보 중 어떤 것을 cell state에 저장할 것인지를 정한다.
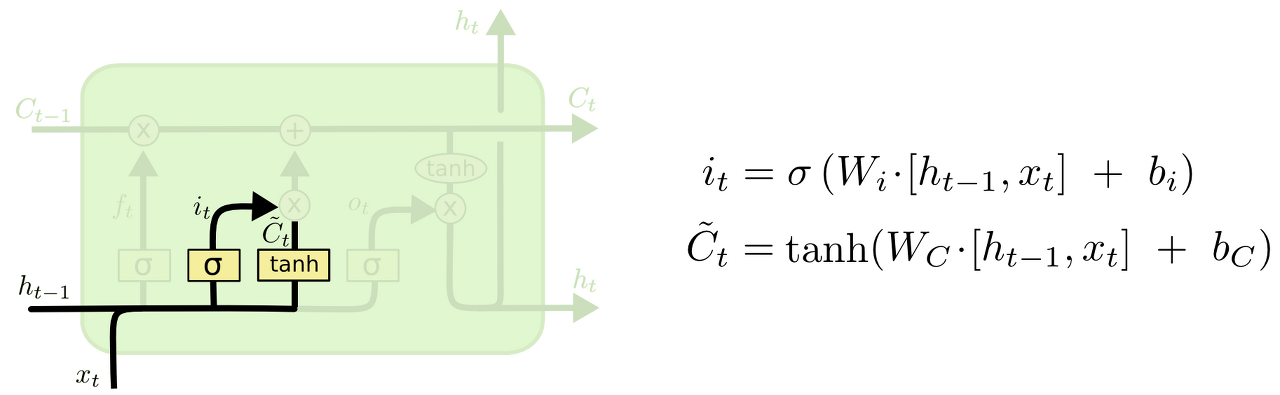
먼저, "input gate layer"라고 불리는 sigmoid layer가 어떤 값을 업데이트할 지 정한다. 그 다음에 tanh layer가 새로운 후보 값들인 라는 vector를 만들고, cell state에 더할 준비를 한다. 이렇게 두 단계에서 나온 정보를 합쳐서 state를 업데이트할 재료를 만들게 된다.
ex) 기존 주어의 성별을 잊어버리기로 했고, 그 대신 새로운 주어의 성별 정보를 cell state에 더하고 싶을 것이다.
3. 이제 과거 state인 를 업데이트해서 새로운 cell state인 를 만든다.
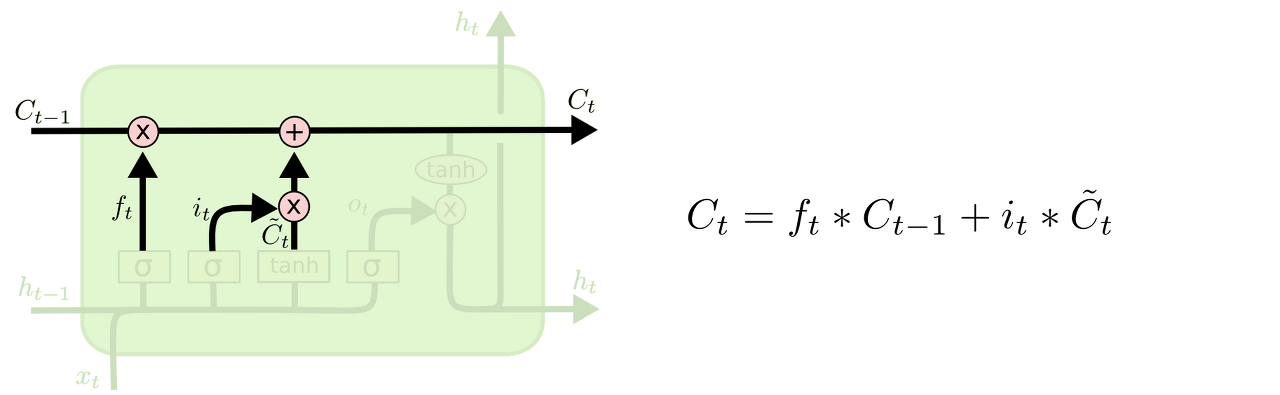
이미 이전 단계에서 어떤 값을 얼마나 업데이트해야 할 지 다 정해놨으므로 여기서는 그 일을 실천만 하면 된다.
우선 이전 Cell state에 를 곱해서 가장 첫 단계에서 잊어버리기로 정했던 것들을 진짜로 잊어버린다. 그리고 를 더한다. 이 더하는 값은 두 번째 단계에서 업데이트하기로 한 값을 얼마나 업데이트할 지 정한 만큼 scale한 값이 된다.
ex) 이 단계에서 실제로 이전 주어의 성별 정보를 없애고 새로운 정보를 더하게 되는데, 이는 지난 단계들에서 다 정했던 것들을 실천만 하는 단계임을 다시 확인할 수 있다.
4. 무엇을 output으로 내보낼 지 정한다.
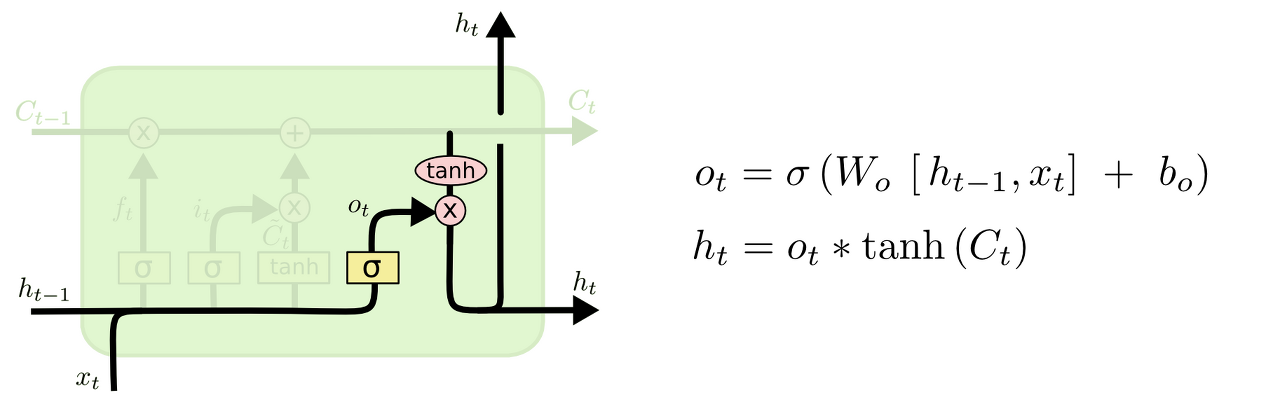
이 output은 cell state를 바탕으로 필터된 값이 될 것이다. 가장 먼저, sigmoid layer에 input 데이터를 태워서 cell state의 어느 부분을 output으로 내보낼 지를 정한다. 그리고나서 cell state를 tanh layer에 태워서 -1과 1 사이의 값을 받은 뒤에 방금 전에 계산한 sigmoid gate의 output과 곱해준다. 그렇게 하면 우리가 output으로 보내고자 하는 부분만 내보낼 수 있게 된다.
ex) 우리는 주어를 input으로 받았으므로 주어 다음에 오게 될 예측값인 output으로 적절한 답은 아마도 동사 개념의 무언가가 될 것이다. 예를 들어 최종적인 Output은 앞에서 본 주어가 단수형인지 복수형인지에 따라 그 형태가 달라질 수도 있는 것이다.
extra
기본적인 LSTM 모델의 작동 방식에 대해서 알아보았다. LSTM이라고 해서 모두 동일한 구조를 가지는 것은 아니고, 논문에 따라서 제각각 조금씩 다른 버전을 채용하고 있다. 차이점들은 사실상 미미하지만 어떤 문제에 어떤 모델을 쓰느냐에 따라 미세한 결과 차이가 존재한다고 한다. 다음과 같은 여러 모델들의 예시가 있다.
1. peephole connection 추가 모델
: 모든 gate마다 엿보기 구멍을 달아놨는데, 논문마다 어디에는 엿보기 구멍을 달고 어디에는 안 달고 할 수가 있다. 그림에 그려과 같이 연결을 통해 이전 time step의 cell state 상태가 입력으로 추가되며, 좀 더 많은 context를 인식할 수 있다.
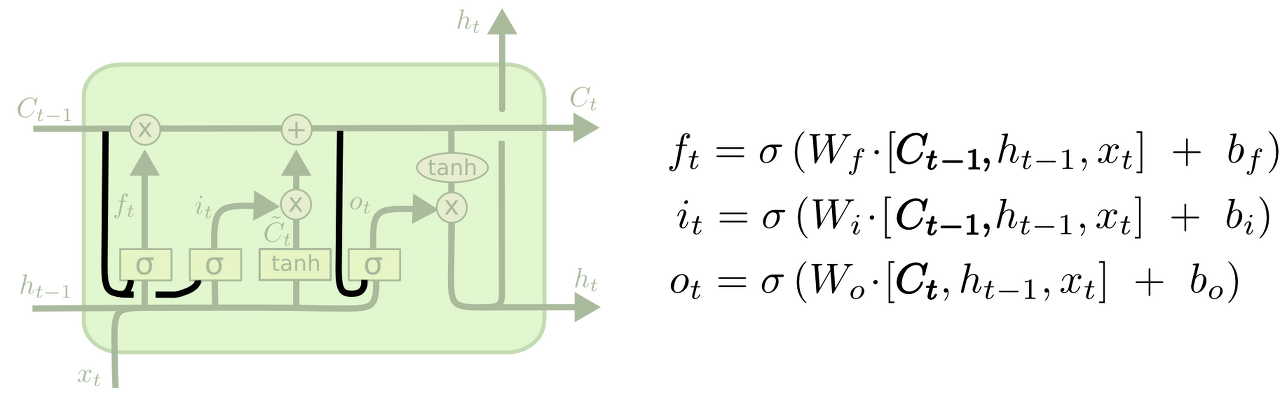
2. Forget gate와 input gate가 합쳐진 다른 변형 모델
: 무엇을 잊어버릴지와 새로운 정보를 어느 부분에 더할 지를 따로 생각하지 않고, 한 번에 결정을 내리는 것이다. 이 모델은 새로운 정보가 들어가는 자리만 잊어버리고 이전 정보를 잊어버리는 부분만 새로운 값을 넣게 된다.
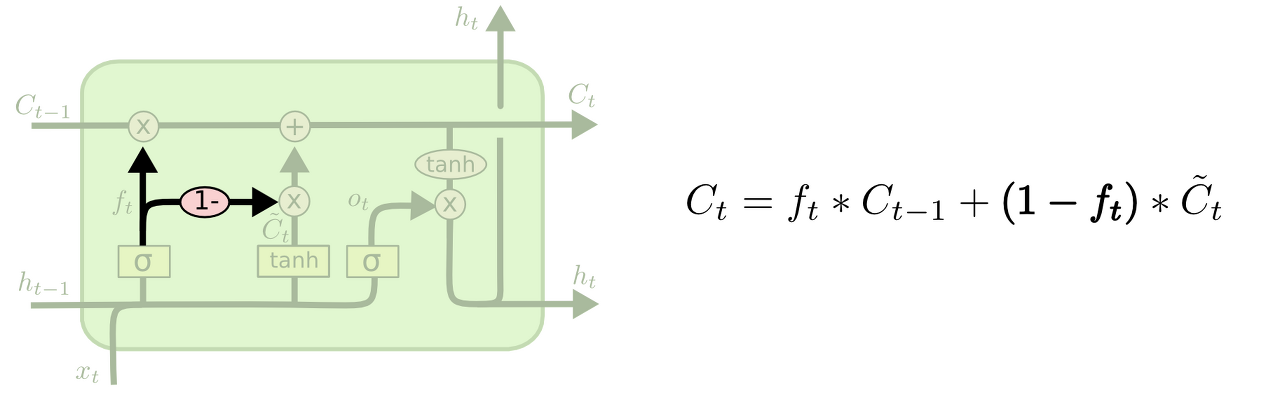
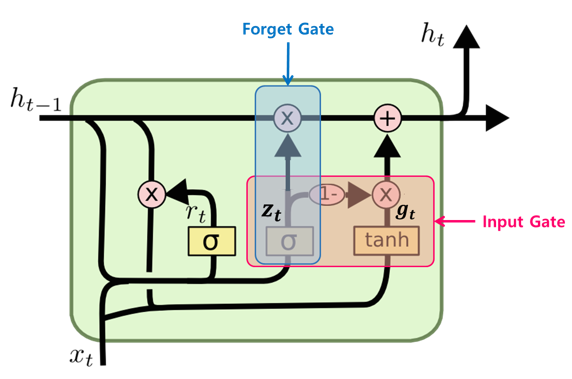
GRU
LSTM cell의 간소화된 버전이라고 할 수 있으며 아래와 같은 구조를 가진다. GRU는 LSTM보다 학습 속도가 빠르다고 알려져있지만 여러 평가에서 GRU는 LSTM과 비슷한 성능을 보인다고 알려져 있다. GRU와 LSTM 중 어떤 것이 모델의 성능면에서 더 낫다라고 단정지어 말할 수 없으며, 기존에 LSTM을 사용하면서 최적의 하이퍼파라미터를 찾아낸 상황이라면 굳이 GRU로 바꿔서 사용할 필요는 없다고 한다. 데이터 양이 적을 때는, 매개 변수의 양이 적은 GRU가 조금 더 낫고, 데이터 양이 더 많으면 LSTM이 더 낫다고 알려져 있다. GRU보다 LSTM에 대한 연구나 사용량이 더 많은데, 이는 LSTM이 더 먼저 나온 구조이기 때문이라고 한다.
이 모델은 forget gate와 input gate를 하나의 "update gate"로 합쳤고, cell state와 hidden state를 합쳤고, 또 다른 여러 변경점이 있다. 결과적으로 GRU는 기존 LSTM보다 단순한 구조를 가진다.
References
'논문 리뷰 > Neural Network' 카테고리의 다른 글
| Multivariable Linear Regression + nn.Module (0) | 2021.03.02 |
|---|---|
| Simple Linear Regression + Cost func / GD (0) | 2021.03.02 |
| Neural Network + Activation func (0) | 2021.03.02 |



댓글