사람이 1시간 동안 공부했을 때 2점, 2시간 공부했을 때 4점, 3시간했을 때 6점을 받는다는 training dataset이 존재한다고 가정한다. 그렇다면 test dataset으로 4시간 공부했을 때 몇점을 얻을 수 있겠는가에 대한 질문에 답해보자.
: 우리는 4시간 공부했을 때 8점을 받을 수 있다고 쉽게 예측할 수 있다.

Simple Linear Regression(선형 회귀)란?
: 학습 데이터와 가장 잘 맞는 하나의 직선을 찾는 것으로 보통 H(x)=Wx+b의 형태를 가진다.
이때 x와 곱해지는 W를 weight(가중치), b를 bias(편향)이라고 표현하고 simple linear이기 때문에 x는 1개이다.
Cost function(비용 함수)란?
: 실제 training dataset과 그 dataset를 가장 잘 표현하는 직선과의 차이
비용 함수(cost function) = 손실 함수(loss function) = 오차 함수(error function) = 목적 함수(objective function)

위 그림에서 4개의 점이 training data를 의미하고 서로 다른 W와 b의 값에 따라 그려진 3개의 직선 중 가장 비슷하게 그려진 직선은 검은색 직선이지만 수학적인 근거를 위해 error(오차)라는 개념이 도입되게 된다.

주황색 선에 대해서의 실제값과 직선의 예측값(동일한 x값에서의 직선 y값)에 대한 차이를 화살표 ↕로 표현한 상태이다. 각 실제값과 각 예측값과의 차이고 이를 각 실제값에서의 error라고 말할 수 있다.
error의 총합을 구할 때, 음수와 양수가 섞여있으므로 정확한 오차의 크기 측정이 불가능하다. 따라 각 오차들을 제곱해 준 뒤에 전부 더해주고 데이터의 개수인 n으로 나누는 방식을 취하는데 Mean Squared Error, MSE(평균 제곱 오차)라고 부른다.
평균 제곱 오차를 W와 b에 대한 비용함수로 재정의하여 표현하면 다음과 같다.

Cost function(MSE 방식으로 구한 오차의 합)은 Gradient Descent를 사용하여 오차값을 최소로 만드는 W와 b를 찾아낼 수 있다. 이때 가중치 W는 직선에서의 기울기를 의미한다.
Gradient Descent(경사하강법, optimizer)란?
: cost function를 미분하여 현재 W에서의 접선의 기울기를 구하고, 접선의 기울기가 낮은 방향으로 W의 값을 변경하는 작업을 반복하는 방식
W와 cost의 관계를 그래프로 표현하면 다음과 같은 convex가 나온다.

여기서 W의 최소값을 찾기 위해서는 맨 아래 볼록한 지점에서의 W 값을 찾아야 한다. 기계는 임의의 초기값 W를 정한 다음 맨 아래 지점까지 W 값을 수정해 나간다. 이때 우리는 고등학교 때 배웠던 한 점에서의 순간변화율(접선에서의 기울기)의 개념을 사용하여 경사하강법을 사용한다.

맨 아래 볼록한 지점에서의 순간변화율은 0이고 그래프 상으로는 초록색 직선이 x축과 평행한 상태이다. 즉, cost가 최소화 되는 지점은 접선의 기울기가 0이 되는 지점이며, 미분값 또한 0이 되는 지점이다.
결국 경사하강법의 아이디어는 cost function를 미분하여 현재 W에서의 접선의 기울기를 구하고, 접선의 기울기가 낮은 방향으로 W의 값을 변경하는 작업을 반복한다.
learning rate라고 불리는 α는 어떤 의미를 가질까?
: 기울기를 수정하면서 W +- α*(기울기)를 해주는데, W값을 변경할 때, 얼마나 크게 변경할 지를 결정해주는 값 or W를 그래프의 한 점으로 보고 접선의 기울기가 0일 때까지 경사를 따라 내려간다는 관점에서는 얼마나 큰 폭으로 이동할지 결정하는 값
학습률 α가 지나치게 높은 값을 가지게 되면, 접선의 기울기가 0이 되는 W를 찾아가는 것이 아니라 W의 값이 발산하는 상황이 나타난다. 반대로 학습률 α가 지나치게 낮은 값을 가지면 학습 속도가 느려지므로 적당한 α의 값을 찾아내는 것도 중요하다.
pytorch로 구현한 linear regression 코드를 살펴보자
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
# training data 선언
x_train = torch.FloatTensor([[1], [2], [3]])
y_train = torch.FloatTensor([[2], [4], [6]])
# 모델 초기화
# requires_grad=True로 자동 미분 기능 적용
W = torch.zeros(1, requires_grad=True) # 가중치 W=0으로 초기화, 학습을 통해 값이 변경되는 변수임을 명시
b = torch.zeros(1, requires_grad=True) # 편향 b=0으로 초기화, 학습을 통해 값이 변경되는 변수임을 명시
# optimizer 설정: lr=learning rate 의미
optimizer = optim.SGD([W, b], lr=0.01)
nb_epochs = 2000 # 원하는만큼 경사 하강법을 반복
for epoch in range(nb_epochs + 1):
# H(x) 계산: 직선에 방정식에 해당되는 가설 선언
hypothesis = x_train * W + b
# cost 계산: 선형 회귀 cost function인 MSE 선언
cost = torch.mean((hypothesis - y_train) ** 2)
# cost로 H(x) 개선
# 파이토치는 미분을 통해 얻은 기울기를 이전에 계산된 기울기 값에 누적시키는 특징 존재
optimizer.zero_grad() # gradient를 0으로 초기화해야만 새로운 W, b에 대해 새로운 기울기 계산 가능
cost.backward() # 비용 함수를 미분하여 gradient 계산
optimizer.step() # W, b update
# 100번마다 로그 출력
if epoch % 100 == 0:
print('Epoch {:4d}/{} W: {:.3f}, b: {:.3f} Cost: {:.6f}'.format(
epoch, nb_epochs, W.item(), b.item(), cost.item()
))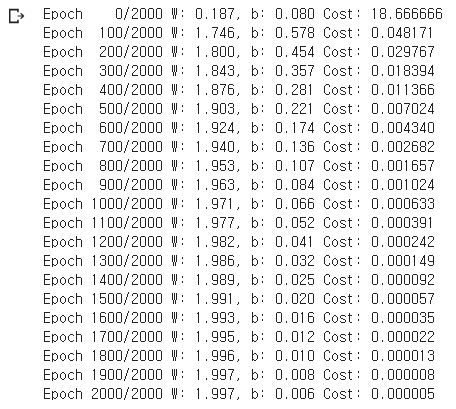
결과값을 보면 W는 2에 b는 0에 수렴하는 것을 확인할 수 있다. lr를 0.01에서 0.1로 바꿔보면 어떨까 싶어서 변경해 보았다. 가중치 변경 폭이 더 커졌기에 더 빨리 수렴하는 모습을 보인다.

그러나 lr를 더 큰 수인 0.2로 바꾸니 다음과 같이 발산해 버린다. 적절한 lr 설정 중요성을 알 수 있다.

위 코드에서는 requires_grad=True, backward()가 나온다. 모델이 복잡해질수록 경사 하강법을 넘파이 등으로 직접 코딩하는 것은 까다로운 일이기 때문에, 파이토치에서는 이런 수고를 하지 않도록 자동 미분(Autograd)을 지원한다. 자동 미분을 사용하면 미분 계산을 자동화하여 경사 하강법을 손쉽게 사용할 수 있다.
import torch
# 값이 2인 임의의 스칼라 텐서 w를 선언, required_grad를 True로 설정
# 이는 이 텐서에 대한 기울기를 저장하겠다는 의미입니다.
# 뒤에서 보겠지만, 이렇게 하면 w.grad에 w에 대한 미분값이 저장됩니다.
w = torch.tensor(2.0, requires_grad=True)
# 수식을 정의
y = w**2
z = 2*y + 5
# 이제 해당 수식을 w에 대해서 미분해야합니다.
# .backward()를 호출하면 해당 수식의 w에 대한 기울기를 계산합니다.
'''
y.backward()
print(w.grad) # 수식을 w로 미분한 값 : 4.0
'''
z.backward()
# w.grad를 출력하면 w가 속한 수식을 w로 미분한 값이 저장된 것을 확인
print('수식을 w로 미분한 값 : {}'.format(w.grad))
# 수식을 w로 미분한 값 : 8.0
'논문 리뷰 > Neural Network' 카테고리의 다른 글
| RNN, LSTM (0) | 2021.05.06 |
|---|---|
| Multivariable Linear Regression + nn.Module (0) | 2021.03.02 |
| Neural Network + Activation func (0) | 2021.03.02 |



댓글