현실의 big scale의 문제들에서는 Q table lookup같은 개념이 불가능할 수 있고, 그에 따른 방법들을 배운다.

model-free big scale 문제에 대해 해결하는 Incremental(점진적), Batch(한번에 해결)하는 방식

다음과 같은 large problems에 RL이 사용되고, 모든 states 마다 table lookup이 불가능하기 때문에 이를 대체하기 위한 방법이 필요하다.
- Backgammon 보드게임: 10^20 states
- 바둑: 10^170 states
- 헬리콥터: continuous states

lookup table기반
- state-value fn V(s) s개수만큼 빈칸이 존재한다.
- action-value fn Q(s,a) s-a pair개수만큼 빈칸이 존재한다.
large MDP에서의 문제
- 너무 많은 state/s-action를 메모리에 저장할 수 없다.
- 담을수 있다고 하더라고 배우는 과정에서의 연산이 너무 느리다.
large MDP solution
- 근사함수를 사용하여 실제 Vpi, Qpi를 학습하려고 하는 것이 목적
V^(s,w) ~~ 실제 value fn Vpi(s)를 모방하는 근사함수
Q^(s,a,w) ~~ 실제 value fn Qpi(s,a)를 모방하는 근사함수
- 내가 보았던 state로 안본 state를 generalise한다.
- w 값 update를 통해 학습한다.
w: V^(s)함수안에 들어있는 파라미터

세 box 모두 w라는 parameter가 관장
- V(s,w): s를 넣었을 때 value를 return
- action in 상태의 Q(s,a,w): s,a를 넣었을 때 value를 return
- action out 상태의 Q(s,an,w): s만 넣었을 때 s에서 할 수 있는 모든 a들에 대해서 여러개의 output를 return

- differentiable(미분가능한) Function Approximator(모방하는 함수)는 뭘 쓸 수 있나?
:linear combinations of features(특성 가중치 합), Neural network
- non-stationary(모분포가 계속 바뀌고) non-iid(독립적이지 않은) data에 대해 적합한 방법을 요구한다.
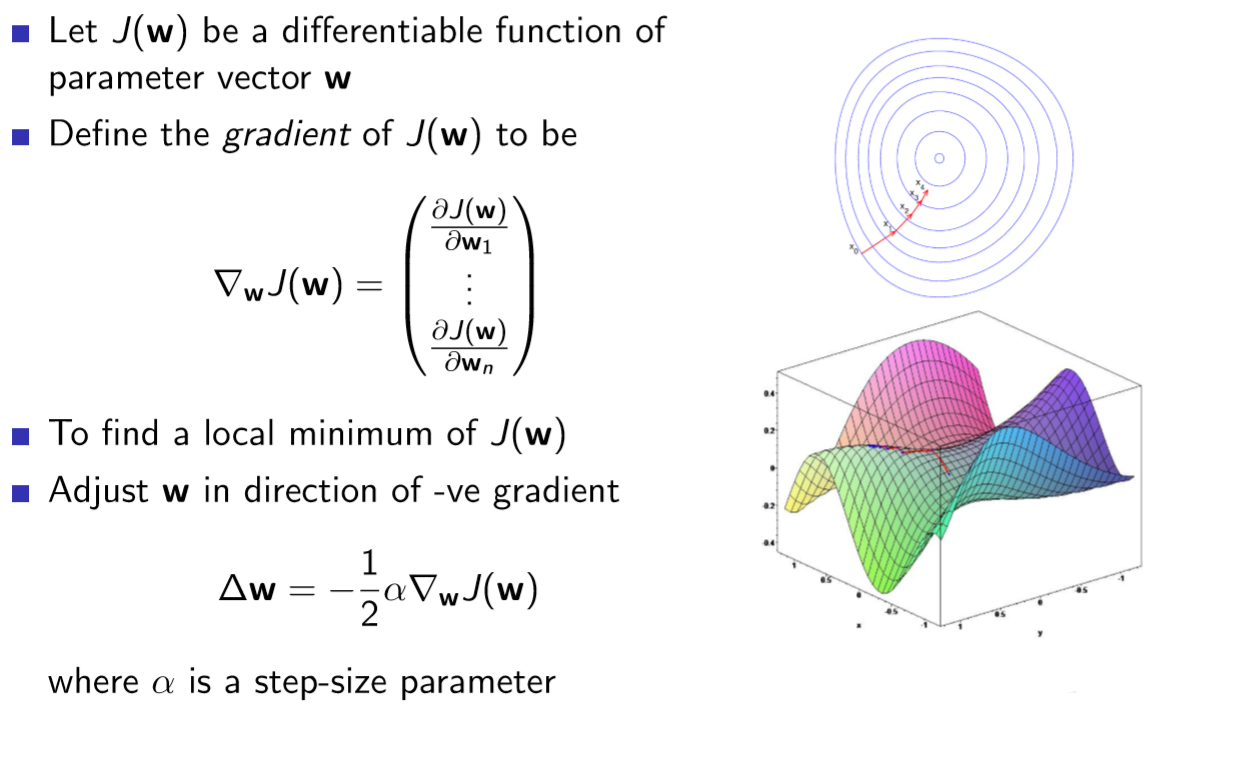
- input이 n차원 vector w인 J(w) 함수가 있다고 가정한다.
- J라는 함수를 최소화 하는 local minimum의 input w를 찾고 싶다.
J라는 함수가 복잡한 함수여서 오른쪽 그림과 같이 그려진다고 하고, 어떤 점부터 시작해서 조금씩 움직여서 J(w)의 높이가 최저점으로 가고싶다. 이때 최저점은 global한 것이 아닌 그 부근에서 제일 작은 점인 local한 최저점이다.
gradient(편미분=기울기)를 구해서 J(w)를 첫번째 항부터 n까지로 미분한 것이 온 것들이 vector 특성의 값들이 되고, 방향을 알려주기 때문에 -로 제일 빠르게 가팔라지는 곳으로 미세한 값 a(step-size)만큼 움직이는 것을 반복해서 그 부근에서 제일 작은 곳으로 가는 방법
step-size a: 어떤 Gradient 방향으로 한번에 너무 많은 이동을 막아야 local minimum이 잘 구해진다.
ex) 밤에 산을 올라갔다가 산이 어떤지 모르고 길을 모르고 내려올 때, 경사가 급한쪽으로 한걸음 내딛고 다음 지점에서 급한쪽으로 내딛는 것을 반복해서 내려오면 운이 좋다면 지상(global minumunm)으로 내려갈 수 있고, 움푹 파인 곳(local minumum)에 갇힐 수도 있다.

- Goal: Oracle이 있어서 true Value fn를 알려주었다고 가정, 목적함수인 J(w)를 줄이는 것이 목적
FA V^(s,w)가 value fn Vpi를 잘 모방하는 것 = 차이가 적다
J(w) = Epi(policy pi를 따랐을 때의 expectation)[(Vpi(s) - V^(s,w))^2]
차이의 제곱하는 이유 = J의 목적함수(실제 s에서 실제 value와 모방한 value의 차이)^2 해주어서 음수를 없게 함
J를 줄이는 방향으로 w를 update해주어야 함
- Gradient descent(미분) 방법으로 local minimum을 찾는다.
J(w) = [(Vpi(s) - V^(s,w))^2]를 w가 V^에 들어가 있어서 w에 대해 미분하고 위에서의 △w식에 대입하면
= a * Epi[(Vpi(s) - V^(s,w))▽wV^(s,w)]: w를 이만큼 update해야함
- Stochastic gradient descent는 gradient를 sample한다.
△w = a(Vpi(s) - V^(s,w))▽wV^(s,w): policy pi를 따라간 sample를 위 expectation식에 넣어줌
sample(방문했던 states)들을 넣어 update해서 expectation과 자연스럽게 같게 하는 방식

linear combination example들을 강의에서 주로 사용
feature들이 존재하고, feature들의 linear combination(w들을 쭉 곱한 값)를 value fn로 쓴다면
- s가 있으면 s에 대해 n개의 feature를 사람이 만들 수 있다.
ex) 주식시장에서의 feature :이동평균선, 전국가...
feature들을 이용해서 그 때의 value fn: 각 feature들에 w들을 가중합한 값 = ∑xn(feature)*wn
X에 S를 넣으면 feature가 나오는 함수라기보다는 feature는 State를 잘 표현해주는 값들인 x1(S)...xn(S)

- feature의 linear combination으로 value fn를 대표한다.
처음의 이상한 값들을 실제값에 근사하게 w를 수정해 나가는 과정
- Objective fn는 true value와 모방함수의 w vector의 내적인 x(S)^T·w으로 구성
J(w) = Epi[(Vpi() - x(S)^T·w)^)2]: 모방함수 자리에 x(S)^T·w가 삽입
- Stochastic gradient descent를 이용해서 학습하면 좋은 점은 linear value fn(선형함수)이기 때문에 global optimum으로 수렴한다.
- Update 규칙은 목적함수를 미분 = step-size a * prediction error * feature value
summary
S의 feature들과 최종 value fn이 어떤 관계에 있을 텐데, 그 관계가 선형이라 가정하고 linear value fn를 사용하여 value fn 학습이 목적 == feature vector들의 linear 합(feature에 w를 내적한)으로 value가 나올 것이라는 가정을 하고 계산
선형으로 모방함수를 구성해서 처음 것보다 나은 w(feature마다의 가중치)를 찾아간다.

David Silver: table lookup은 linear value fn의 한 예시이다. feature를 state 개수만큼 만들고 그에 따른 feature vector들을 만들어서 내적하면, state Sn·Wn으로도 표현이 가능하다. Wn이 각 테이블에 있던 S에서의 값이었던 것

- 지금까지는 true value fn를 Oracle이 알려주었다고 가정하고 수식을 전개했지만, RL에는 supervisor이 없어 실제 value는 모르고 reward만 존재한다.
- Vpi(s)(실제 value 자리)에 지금까지 배웠던 MC와 TD를 대체한다.
- for MC: Vpi(s)자리에 Gt(return)을 삽입하고 sample들을 통해서 w를 update
- for TD(0): Vpi(s)자리에 TD target을 삽입하고 sample들을 통해서 w를 update
현재 step에서 value의 예측치는 next-step에서의 예측치의 합으로 구성
- for TD(lamda): Vpi(s)자리에 Gt(lamda)을 삽입하고 sample들을 통해서 w를 update

- Return Gt는 비편향적인 noisy true value fn이기 때문에 supervised learning의 data로도 사용이 가능하다.
- MC evaluation를 하면 local optimum으로 심지어 non-linear value FA를 할 때에도 variances가 엄청 클수도 있지만 true value 수렴한다.

- TD-target은 편향된 true value fn이고, supervised learning의 data로도 사용이 가능하다.
- Linear TD(0)는 global optimum에 편향되어 있기 때문에 정확한 값이 아닐 수 있지만 거의 가깝게 수렴한다.
Q: 기존 가정에서는 TD-target 자리가 상수 였는데, true value fn을 사용할 때에는 w가 들어가는 함수인데 이대로 미분해도 되는건가?
A: 우리가 update를 할 때, one-step이 정확하다는 가정이 아니고, target 값까지 update하려면 one-step 더 가서 과거를 보는 것과 과거에서 미래를 보는 값이 섞이게 되는데, 이는 전개하기에 매우 어려움(시간 역행하고 섞일 수도 있음)

- TD(0) 방식에 Eligibility traces 값이 추가되어 곱해주는 특징이 존재한다.
이제 Control problems

- Policy evaluation단계에서 Approximate policy evaluation(위에서 배운 내용을 이제 V아니라 Q로 진행)
- Policy improvement단계에서는 e-Greedy policy로 진행

간단하게 위에서 배운 V 내용을 그냥 Q(s,a)로 대체
- 실제 value fn인 Qpi가 있을 때 Q^(s,a,w)로 모방한다.
- 둘 사이의 error의 제곱을 minimise하는 방식으로 진행되고 이를 mean-squared error를 줄인다고 표현한다.
- 목적함수를 미분하여 △w 계산

- 똑같이 feature vector를 생성하여, feature 바탕으로 linear합으로 만들 수 있고 그것을 넣어서 △w update

- 가정했던 true Q 대신에 MC, TD(0), TD(lamda)를 넣을 수 있다.
Q: prediction과 같이 한 것 뿐인데 control이 가능한건가?

Linear한 Value FA를 썼기 때문에 Linear Sarsa라고 함
Linear Sarsa를 이용한 학습 예시: 속도, 위치, 가속 등의 여러 feature들이 존재하기 때문에 매우 어려움

최종 학습 결과: 0인 점들은 방문할 수 없어서 학습하지 못한 환경 == 이 위치에서 이 속도로 학습할 기회가 없었다.

y축이 높을 수록 좋지 않다. lamda 값인 0과 1사이에 sweet spot이 존재하기 때문에 bootstrap이 필요하다.

이런 상황이 되면 TD(0)의 value fn이 아래 그림과 같이 발산하는 경우도 존재한다.


Q: big-scale 상황도 on-policy라고 할 수 있는건가?
- on => off-policy , MC => TD(lamda)로 갈수록 수렴성이 좋지 않다.
linear하게 배운 식들도 non-linear 상황에서 적용이 가능하다고 한다.
이론상 이렇지만 실제 환경에서는 의외로 잘 작동한다고 한다.
Q: TD(lamda = 1)가 MC와 같은 결과 아니었나? 저기서는 0 < lamda < 1 사이의 값을 말하는 것인가?

Prediction 문제에서 on, off policy / linear, non-linear 환경에서도 이론성 수렴성이 완벽한 Gradient TD도 존재한다.
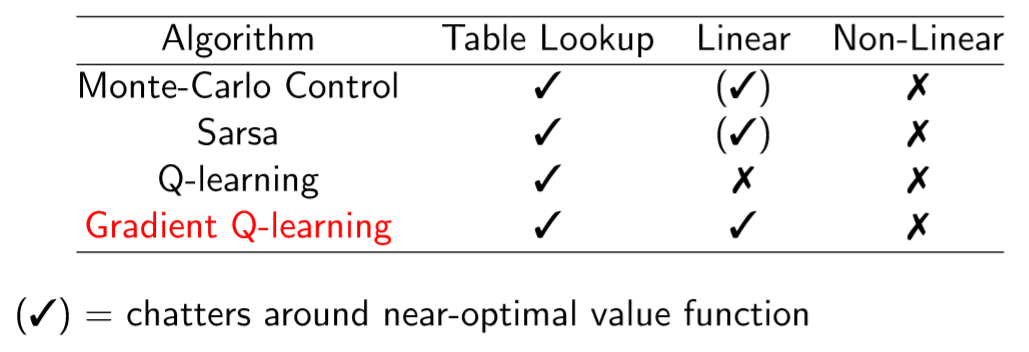
Control문제에서도 동일하게 이론상 수렴하는 Gradient TD

지금까지 봤던 Incremental methods는 gradient descent를 이용해서 sample 하나로 update 하는 방식
- sample로 1번 update하고 버려지기 때문에 이는 효과적이지 않다. sample: s에서 a를 해서 s'에 도착하는 transition
- 이미 agent가 쌓은 경험을 통해 반복해서 쓰면서 학습하는 방식

- Vpi와 같아지기를 바라는 FA V^(s,w) 주어진다.
- <s,a> pairs의 경험인 D가 존재한다.
- 이 경험들을 통해 V^의 w를 best fitting하게 한다.
- Least squares 방법론을 통해 parameter vector인 w를 찾으려고 한다.
Incremental methods에는 expectation에 pi였고, Batch methods에서는 주어진 데이터에 대해 하는 것이기 때문에 D로 바뀌었다. off-policy상태

- D를 가지고 state, value를 sampling하여 stochastic gradient descent(update) 진행한다.
- experience replay: off-policy 방식에서 한 샘플(경험)을 여러개 쓰면서 update를 진행하면 least squares(error값의 제곱의 차이를 줄이는 것)solution에 수렴한다.

앞에서 non-linear 함수들을 쓰면 수렴성이 보장되지 않았다. 이를 잘 수렴하게 하기 위해서 두가지의 trick인 experience replay와 fixed Q-targets를 사용
experience replay
- e-greedy policy로 game을 진행한다.
- s에서 a를 하면 다음 s'가 뭐가 되었는지 transition을 replay memory D에 쌓는다.
- 그 곳에서 random하게 mini-batch transition을 뽑아서 학습한다.
- Least squares를 줄이는 것: T의 target과 Q차이의 제곱을 줄이는 것
fixed Q-targets: target를 고정시킨다는 의미
- TD target를 계산할 때 예전 버전의 parameter를 사용(구버전, 신버전)한다.
update를 할 때마다 방향이 바뀌기 때문에 수렴이 힘들어서 어느정도의 고정상태를 사용하여 n번씩 update해서 parameter set를 두가지 관리. 예전 버전을 w-, 최신 버전을 w
w를 update하는 것인데 target는 w-사용

- 최신 내장의 images가 들어옴 => Convolutional Layer를 거침 => 최종 모든 action에 대한 각 output이 나오는 방식
reward는 score의 변화 / input은 state은 last 4 frames / Q(s,a)는 18 조이스틱, 버튼 position
모든 게임에 대해 network architecture, hyperparameters를 고정시킨 채로 모든 게임들을 학습시켰음
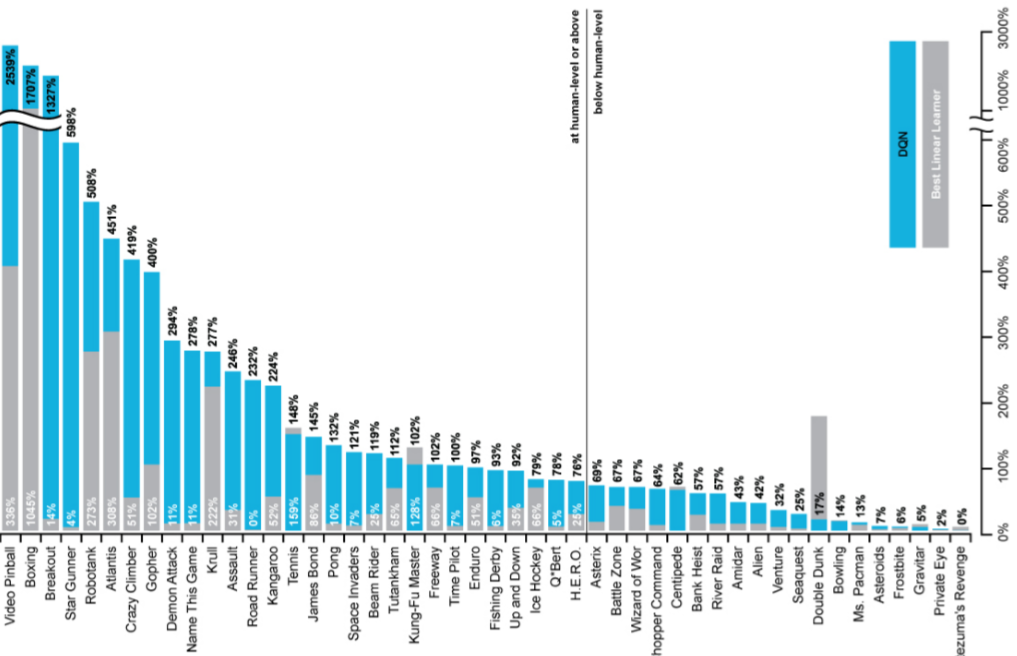
Atari에 여러 종류의 게임이 있는데 파란색이 DQN으로 학습한 방식
대부분의 game에서 우세하며 가운데 선은 사람의 실력을 의미 == DQN이 매우 훌륭하다
Neural net이라는 non-linear 방식, off-policy, MC가 아닌 TD로 학습했기 때문에 수렴하기 힘든 조건에서도 replay memory와 fixed-Q로 학습을 잘 했다

Replay와 Fixed를 사용하면 평균 점수가 압도적으로 오르는 것을 확인 가능
아래는 교재 및 참고 블로그, 유튜브 강좌입니다.
deepmind.com/learning-resources/-introduction-reinforcement-learning-david-silver
Interested in learning more about reinforcement learning? Follow along in this video series as DeepMind Principal Scientist, cre
We research and build safe AI systems that learn how to solve problems and advance scientific discovery for all. Explore our work: deepmind.com/research
deepmind.com
www.youtube.com/watch?v=71nH1BUjhNw&list=LL&index=1&t=3s
'논문 리뷰 > RL' 카테고리의 다른 글
| Vanila Actor-Critic (0) | 2021.03.09 |
|---|---|
| REINFORCE(MC-PG) + vanila Policy Gradient (0) | 2021.03.04 |
| Lecture 7: Policy Gradient (0) | 2021.01.23 |
| Lecture 5: Model-Free Control (0) | 2021.01.18 |
| Lecture 4: Model-Free Prediction (0) | 2021.01.15 |
| Lecture 3: Planning by Dynamic Programming (0) | 2021.01.13 |




댓글