이전 강의의 model-based(MDP, env를 모두 다 알 경우의) DP와는 다르게 model-free prediction 방식을 공부한다.


Monte-Carlo방식: 계속된 실행으로 도출한 실제 값들을 통해서 추정하는 방식 의미
policy는 정해져있고, n번 시행한 뒤 나온 모든 값들을 평균함
- 경험으로 부터 직접 배운다.
- model-free: MDP transitions/ rewards를 몰라도 가능하다.
- episode가 끝나야 return이 정해지고, 그 값들을 평균낸 것이 value
- 계속 loop한 episode의 경우는 return이 나오지 않으므로, episode는 종료되어야만 한다.

- Goal: Vpi를 episode로 부터 배우는 것
- return은 discounted reward의 total이다.
- value fn는 return의 기댓값이다.
- MC Policy Evaluation는 실제로 실행하여 도출한 평균을 사용한다.
MC에는 2가지 방식이 존재


state s를 evaluate하기 위해서는 방문할 때마다 해당 s에 count를 늘려주고, episode가 끝날 때 return를 적어준다.
한 episode에서 s에 여러번 방문이 가능한데, 여러번 방문 한것을 다 쳐주는 것이 every visit이고 처음의 방문만 쳐주는 것이 fitst-visit이다.
- First-visit: episode에서 처음 방문할 때만 counter를 올려주고, 그때만 return을 더해서 평균해준다.
- 대수의 법칙에 인해 n이 무한으로 가면 V(s)는 Vpi(s)로 수렴
- Every-visit: episode에서 매번 방문할 때마다 counter를 올려주고, 그때마다 return을 더해서 평균해준다.
- 두 방식 모두 모든 state를 방문한다는 가정하에, 대수의 법칙에 의해 두 방식의 결과는 같다.

Black Jack rule: 내 카드 2장을 받고, 더 받을수도 있고 멈출 수도 있음. 딜러와 내기를 하는데 최종 21이 가까우면 이기고, 21을 넘어가면 무조건 짐. 딜러는 판단을 위해 두장 중 한장 오픈하라고 지시
- agent의 state는 정확한 정의가 필요하다.
현재 내 카드의 합은 (12~21) 사이의 수이다.
딜러가 어떤 카드를 보여줄 것인가.
내가 쓸수 있는 ace카드가 있는가: 1또는 10으로 사용이 가능하다.
- Action stick: 카드를 더 안받고 종료한다.
- Action twist: 카드를 더 받는다.
- Reward for stick: 딜러보다 21을 넘지 않으면서 숫자합이 더 크면 +1, 같으면 0, 작으면 -1
- Reward for twist: 21을 넘으면 지기 때문에 -1
- Transitions: 두 카드의 합이 12미만이면 한장을 더 받는다.
이러한 조건에서의 Perdiction Problem을 해결해야 함.

- 내 카드 합이 20 이상이면 stick하고 20이하이면 twist하는 바보같은 Policy를 지정해주어야 한다:
x축 dealer showing / y축 player sum
policy따라 10000번 진행했을 때, usable ace가 있을 경우에 값이 들쭉날쭉함(학습 아직 x)
policy따라 500000번 진행했을 때, usable ace가 있어도 값이 평균화 되어 Vpi가 도출(Prediction 학습 완료)

Uk = 1/k(X1~Xk까지의 합)
=1/k(이 전까지의 합 + Xk)
새로운 값이 나올때마다 이런 수학적 식을 이용하여 추가하며 update할 수 있음

- V(s)를 방문할 때마다 Incremental Mean를 통해 update한다.
N(St) <= N은 방문할 때마다 +1
V(St) <= 이전 값 + 1/N(Gt-V(St))
이전 값이 존재하고, 현재 나온 수치와 새로나온 값의 차 만큼만 더해 update해준다.
- non-stationary problems(MDP가 계속 바뀌는 env)에서는 1/N을 a와 같은 작은 값으로 고정하는 것이 좋을 수 있다.
1/N은 N이 커질수록 계속해서 작아지기 때문에 a로 고정하는 의미: 오래된 경험은 삭제시키고 1/N은 최신 기억이 쌓일수록 update가 되는 것을 보정시켜서 최신값으로만 evaluate하게 만든다.

- 경험으로부터 직접적으로 배운다
- model-free: MDP / rewards에 대한 지식이 필요가 없다.
- 완벽하게 끝나지 않는 episode에서도 learning이 가능하다.
- one-step 뒤의 guess로 지금의 guess를 update한다.

- MC: Gt의 방향으로 V를 update
- TD: R+rV 방향으로 V를 update
- TD Target: Rt+1 + rV(St+1) // one-step 더 가서의 예측치
- TD error: dt = Rt+1 + rV(St+1) - V(St) //V(St): one-step 더 가서의 value 예측치 - V(St+1): r * one-step 에서의 value 예측치
현재 state인 St에서 reward를 예측하는 것
one-step을 더 가서 예측하는 것이 정확하므로, 그 방향으로 V를 update

현 step에서 실제로 걸린 시간 | 도착 예정 시간 | 현 step에서 실제 걸린 시간 + 도착 예정 시간

현 step에서 실제 걸린시간 + 도착 예정 시간
MC: 끝나고 났더니 실제 43분이 걸렸으므로 각 state를 43분으로 update => total time을 도착하고 나서 update
TD: 매 step마다 예측하는 시간이 달랐으므로 예측치로 update => 이전 step을 통해 state마다 update

- TD: final outcome이 나오기 전, incomplete sequences에서 학습 가능
continuing(non-terminateing) 환경에서 사용 가능
- MC: final outcome의 return값이 나온 뒤, complete sequences에서 학습 가능
episodic(terminating) 환경에서 사용 가능

- MC: Gt의 비편향 추정량이 Vpi(St) = Gt를 계속 평균해서 수렴하면 Vpi
- TD: 전지전능한 Oracle이 Vpi(St+1)의 실제값을 알려준다면 Rt+1 + rVpi(St+1)도 비편향 추정량인 Vpi(St)이다.
- 실제로는 Vpi(St+1)의 값을 알지 못하기 때문에, 현재 추측치인 V(St+1)를 update하는데 이는 편향된 추정이다.
- TD의 한 step은 return까지의 모든 random transition, reward 결정보다 적기 때문에 variance가 적음
계속 평균해 수렴한다고 해도 biased 되어있기 때문에, Vpi가 될 보장이 없다.
biased 관점에서는 MC > TD
variance(분산: 확률 변수에서 퍼져있는 정도) 관점 MC < TD

MC: variance가 크고, bias가 0
- 수렴 성질이 뛰어나다(function approximation(딥러닝)을 써도)
- initial value에 sensitive하지 않다.
- 이해하기 쉬고, 사용하기 쉽다.
TD: variance가 작고, bias가 있다.
- MC보다 보통 더 효과적이다.
- TD(0)는 Vpi(s)에 수렴한다.
- Initial value를 통해 update하기 때문에 초기 추측치에 대해 민감하다.
David Silver: biased 되어 있으면 알고리즘이 동작하나? 다행히도 동작한다.

state ABCDE + terminal state 존재, E쪽에 가까울 수록 value가 높을 것
0 => 1 => 100 번 episode를 학습 시킬 때마다의 value 수렴 곡선

여러 a값에 의한 MC와 TD 곡선 예시
episode가 진행됨에 따라, 실제 value를 알기 때문에 그 차이를 계산하고자 RMS 지표로 각 state마다 차이를 평균
episode가 진행됨에 따라 error가 점점 줄어든다. MC는 완만히 줄어들고 TD는 a에 따라 진동하는 모습 관찰

- episode를 무한번 뽑아낼 수 있으면 MC와 TD가 수렴한다.
k개의 제한된 episode만 뽑을 수 있으면 MC와 TD가 같게 수렴할까?

- state는 A, B두개, 8개의 episode 예시
model-free이므로 규칙을 모르는 상태에서 어떤 state에서 reward만 얻은 경험만 존재
이때 V(A), V(B)의 값은? A: 0 B: 0.75
경험의 결과로 오른쪽 그림과 같은 MDP 추측 가능
MC를 이용한 학습: V(A) = 0
TD를 이용한 학습: V(A) = 0.75 [A의 reward 0 + 1 * B의 V(St+1)]
아래는 위 MC, TD의 V(A)를 구한 계산 식인데 적당히 보고 넘어가도 될듯


- TD는 Markov property를 사용해서 value를 추측, Markov env에서 더 효과적
- MC는 Markov property를 사용하지 않고, non-Markov env에서 보통 효과적

St에서 시작해서 다양한 branches가 존재하는 tree 구조
MC는 어느 한가지를 끝까지 해봐서 이 값으로 St를 update

TD는 한 step만 가보고, 그 상태에서 추측해서 update = bootstrapping

DP는 Sampling(끝까지)해보지 않고, 그 칸에서 할 수 있는 모든 actions에 대해서 한 step 가보고, 그 칸에 적혀 있는 value로 full-width update

Bootstrapping: 추측치로 추측치를 update
- MC는 끝까지 가기 때문에 안함 / DP와 TD는 한 step만 가서 하기 때문에 적용
Sampling: 한 sample를 통해 update
- MC, TD는 Sample를 통해 적용 / DP는 그 state에서 가능한 모든 action들을 하기 때문에 안함

x축 Bootstrapping을 하냐, y축 Sampling을 하냐(model-based 상태에서 agent가 policy를 따라 움직이냐)
Exhaustive: 모든 경우의 수를 다 해보는 방법(강화학습 x, 비용이 너무 커서 학습과는 거리가 멀음)

- TD에서 미래의 n-step만큼 가서 update가 가능하고, n이 무한으로 가는 TD = MC이다.

n=1(TD) / n = infinite(MC)
Gt(n) = Rt+1 + rRt+2 + ... + r^n V(St+n)
n개의 reward를 넣고, St+n에서의 추측치를 넣음
n-Step TD error: TD error가 Gt가 Gt(n)으로 교체됨

TD 1... TD 1000까지 10개의 epsode 를 통해a값 바꿔가며 값 비교
details: ONLINE: 움직이는 도중에 update / OFFLINE: 끝나고 update
그래프가 아래로 갈수록 좋은 것인데 1이 제일 좋지도, 1000이 제일 좋지도 않고 3, 5 step-TD가 좋은 것을 볼 수 있다. TD 구간 사이의 sweet spot이 있기 때문에 적절하게 n-Step을 설정 해주어야 한다.

- 다른 n-Step에서 n-step returns를 평균낼 수 있다.
2-step과 4-step를 평균낸 것을 쓰면 안되냐?
- 다른 time-steps의 정보를 효과적으로 섞을 수 있다.

- TD lamda: TD(0)부터 MC까지 모든 것을 평균내도 가능하다. 실제로 많이 쓰이고 논문에도 많음
- (1-lamda)에 lamda를 계속해서 곱해주는 방식, lamda가 곱해지며 MC에 갈수록 가중치가 점점 줄어드는 방식
lamda가 0~1사이의 값이면 이 무한급수의 합은 1이다.
Gt(lamda)를 정의할 수 있고, 정답자리에 넣어서 update가능하다.
Fowardview TD lamda(미래지향), Backwardview TD lamda(과거지향) 두가지 방식이 존재

- 시간이 지날수록 가중치가 점점 줄어든다.
Geometry means를 사용하면 computation를 efficient하게 memoryless하게 사용할 수 있다.
TD(0)와 같은 비용으로 TD(lamda)를 계산 가능하다.
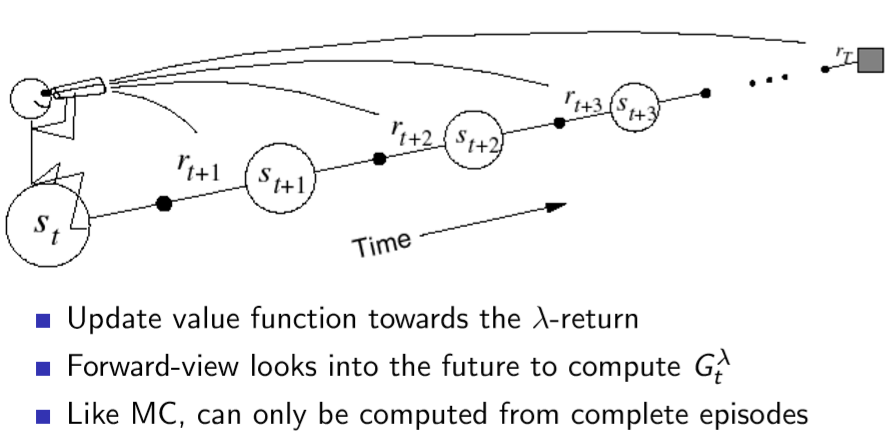
- Foward-view TD(lamda): 내가 현재 St에 있는 상태에서, 미래를 보고 update하는 방식
- 단점: MC와 똑같이, TD(infinite)를 알아야 하므로 episode이 끝난 뒤에 update가 가능 = TD(0)의 장점이 사라짐

- lamda값에 따라 조금씩 달라진다.
lamda를 정해주는 것이 problem 위 그래프에서는 0.9가 가장 efficient

Backward TD(lamda): 매 step마다 online하게 update+ incomplete sequence에서 할 수 있는 TD(0)의 장점 보유

책임이 큰 것한테 update를 많이 해주는 방식
- Frequency heuristic: 책임을 많이 일어난 state에게 물어야 한다.
- Recency heuristic: 책임을 가장 최근에 일어난 state에게 물어야 한다.
- state 별로 Eligibility traces 값을 가지고 있는데, 그 state에 방문유무에 따라 값이 변동되어 저장된다.
한번도 방문하지 않으면 0. state를 방문하면 1를 더해주고 방문하지 않으면 r곱해서 줄인다.

- Et(s): 어느 시점 t일 때, s의 Eligibility traces 값
- value를 매번 update하는데, TD error 값은 TD(0) 값을 그대로 쓰고,
V(s) = V(s) + a * (TD error) * Et(s)(Eligibility traces 값): TD(lamda)와 동일한 값
- 과거에서 책임 소재를 계속 기록하며 오기 때문에, 매 state마다 update가 가능
대부분의 환경에서 Backward TD(lamda)를 주로 사용

lamda = 0: TD(0)와 동일

lamda = 1: MC와 동일
TD(lamda)는 offline update하면 forward-view와 backward-view가 같다.
최근에는 online해도 같다는 연구결과가 있다고는 함
아래는 교재 및 참고 블로그, 유튜브 강좌입니다.
deepmind.com/learning-resources/-introduction-reinforcement-learning-david-silver
Interested in learning more about reinforcement learning? Follow along in this video series as DeepMind Principal Scientist, cre
We research and build safe AI systems that learn how to solve problems and advance scientific discovery for all. Explore our work: deepmind.com/research
deepmind.com
www.youtube.com/watch?v=47FyZtBRglI&list=LL&index=2
'논문 리뷰 > RL' 카테고리의 다른 글
| Lecture 7: Policy Gradient (0) | 2021.01.23 |
|---|---|
| Lecture 6: Value Function Approximation (0) | 2021.01.19 |
| Lecture 5: Model-Free Control (0) | 2021.01.18 |
| Lecture 3: Planning by Dynamic Programming (0) | 2021.01.13 |
| Lecture 2: Markov Decision Processes (2) (0) | 2021.01.05 |
| Lecture 2: Markov Decision Processes (1) (0) | 2021.01.05 |




댓글