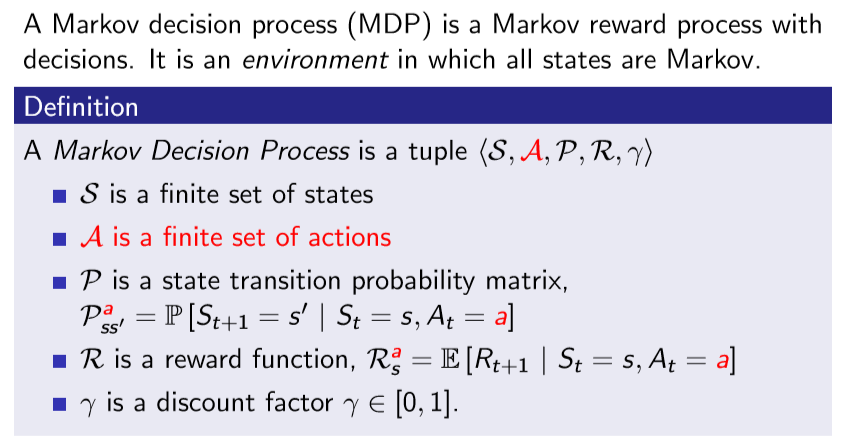
MRP + action = MDP, 모든 state는 Markov함
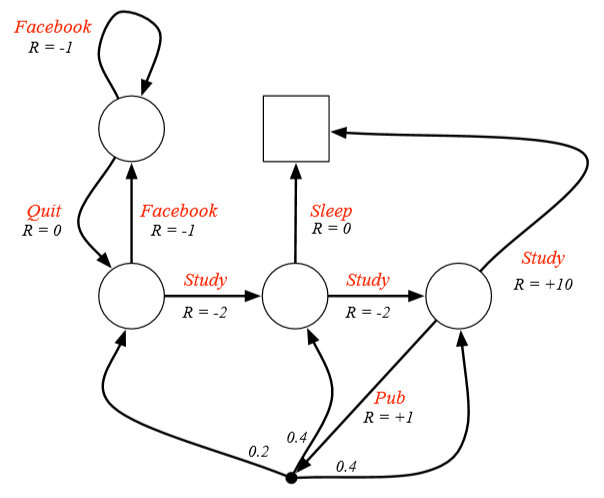
state가 아닌 action마다 reward가 주어짐
action을 한다고 해서 무조건 transition하는게 아니라, 확률적으로 state로 이동함
ex) Pub action의 경우 확률적 다음 state로 이동
MDP는 env꺼고, policy는 agent에 속하므로 위 topology에서는 policy없이 MDP 상태만 표시한 것

MRP에서는 action을 안하기 때문에 policy가 없었음
MDP를 풀이한다는 것 == 어떤 policy를 통해 reward를 최대로 만들 것인가
policy는 St에 있을 때 At을 할 확률
- policy는 agent의 행동을 결정해 준다.
- MDP policy는 현재 state만을 의지한다.(Markov함)
- policy는 stationary하고 시간에 독립적이다.

MDP에서 agent가 어떤 고정된 policy를 가지고 움직인다고 가정
어떤 state에 있을 때, 다음 transition이 어디가 될지 확률을 계산 가능한데 이 과정을 엮어서 Markov하게 볼 수 있다고만 알아두면 될듯, 추가로 1장에서의 Markov state에는 action이 존재하지 않았음
- S1, S2, S3.. 와 같은 state sequence는 Markov Process하다. <S, P>
다음 s'으로 갈 확률 = Σ(s에서 a를 할 확률 * a를 했을 때 s'으로 갈 확률)
- S1, R2, S2, R2.. 와 같은 state, reward sequence는 Markov Reward Process하다. <S, P, R, r>
s에서 얻게되는 Reward = Σ(s에서 a를 할 확률 * a를 했을 때 s에서의 reward)
Agent의 policy가 고정된 상태에서의 진행의 일부는 MP로 또는 MRP로 볼 수 있다.

MRP에 action이 추가되었으므로, pi가 추가되어 특정 policy를 따라갔을 때의 v(s)를 계산
- state-value function: s에서 input이 state만 들어갔을 때
- action-value function: s에서 input이 state와 action 모두 들어갔을 때,,state s에서 action a를 했을 때, 그 이후 pi에 따라 끝까지 진행했을 때 return의 기댓값 == q함수라고 하기도함
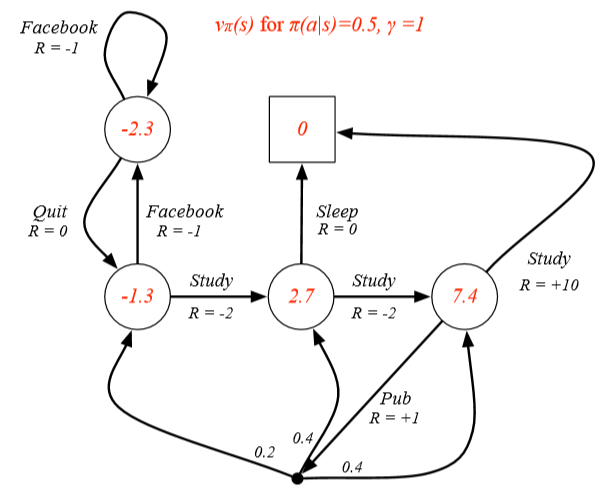
모든 state에서의 action 확률이 1/2라는 policy를 따랐을 때, state value-function 계산

저번 게시글에서 정의했던 Bellman Equation을 MDP의 state/action value-function에도 적용가능하다.
2021/01/05 - [Reinforcement-Learning] - Lecture 2: Markov Decision Processes (1)
- Bellman Equation: value function은 즉시 reward인 Rt+1과 나머지 discounted value인 r*v(St+1)로 분해된다.
똑같은 방식인데 v와 q의 차이만 존재하고, 두 방식 모두 r 로 가중치를 곱해줌
- state-value function은 한 step 뒤 reward를 하나 받고, state부터 pi를 따라 가는 것과 똑같다.
- action-value function은 한 step 뒤reward를 하나 받고, state부터 다음 action을 하는 기댓값과 같다.
Bellman Equation으로 한 step 진행 시 어떤 관계에 있는지 풀어쓴 관계

V를 Q로 수식 표현
Vpi(s): = state에서 action할 확률 * action-value function인 Qpi 의 가중치 합

Q를 V로 수식 표현
Qpi(s,a) = Ras + r * {ΣPass' * Vpi(s')}
s에서 a를 한 value = s에서 a한 reward + r * {Σ s'이 될 확률 * s'에서의 value}
어떤 state에 떨어질지 모름 => 모든 state에 대해 각 state에 떨어질 확률* 그 state에서의 value를 모두 더한 것
Qpi(s,a): s에서 a를 했을 때 pi를 통해 끝까지 진행했을 때의 return의 기댓값
Ras: s에서 a를 했을 때의 reward
Pass': state에 떨어질 확률 = s에서 a를 하면 s'이 될 확률
Vpi(s'): 떨어진 state'에서의 value
위 두 관계식을 서로 대입하면 다음 전개식이 나온다는 것 정도만 알면될듯
검은 점이 action, 흰 원이 state



이러한 계산 과정을 걸쳐 Expectation을 구한다.
7.4 = 0.5 * 10 + 0.5 * (1 + 0.2 * -1.3 + 0.4 * 2.7 + 0.4 * 7.4)

Bellman Expectation Equation을 이용해서 MRP에서의 direct solution 형태와 동일하게 표현
Bellman Equation을 이용하여 MDP에서 value function을 풀었으나 big MDP에서는 direct solution 사용불가능
지금까지 value function만 구했고, action에 대한 건 구하지 않음
지금까지는 주어진 policy에 대한 value function 만을 구했음(sampling) == Bellman Expectation Equtaion

Optimal state-value function: V*(s)는 어떤 policy를 따랐을 때, 최고의 value function을 도출하는 방식
Optimal action-value function: Q*(s)는 MDP에서 할 수 있는 가장 좋은 성능의 action value-function 도출, 할 수 있는 모든 policy을 따른 q(s,a)함수 중에 max값 == 이걸 아는 순간 MDP는 풀림



- partial ordering: 모든 state에 대하여 Vpi(s) > Vpi'(s) 클 때
두 policy가 있을 때 뭐가 더 나은지 비교하는 방법이 필요, 항상 어떤 것이 더 나은 것이라고 판단이 가능한 것은 아님
MDP에서 Optimal Policy가 존재한다는 것은 이미 증명되어있음
Optimal Policy 충족 조건
- 모든 pi에 대해, pi* >= pi가 성립
- Vpi*(s)를 따라가면 V*(s)와 같은 결과
-Qpi*(s,a)를 따라가면 Q*(s,a)와 같은 결과

- Q*(s,a)를 아는 순간 최소 1개의 Optimal Policy를 알 수 있음 => Q*가 s에서 어떤 a를 해야하는지 알려주기 때문
Q*의 action할 확률이 1이고, 나머지가 0인 policy가 있다고 가정하면 그건 Optimal policy
- 모든 MDP 문제에서는 결국 deterministic optimal policy가 존재(실제로는 Stochastic한 문제여도)
- 우리가 Q*를 안다면, 우리는 즉시 Q* 따라만 가면 Optimal policy를 가진다

빨간 선들이 Optimal Policy
이 선들을 찾는 것이 강화학습의 목적
Optimal Policy에서 Bellman Equation을 적용

Bellman Equation과 같은 식인데 max로 바뀜 => maximise하는 action을 선택하는 policy
s에서의 optimal value = q*의 max action을 선택하면됨

Bellman Equation과 똑같은 식인데 V*(s)로 바뀜
이 관계식을 서로 대입하면

이 식은 max 때문에 linear 방정식이 아니다(max는 최대값을 고르는 것이기 때문에 선형적이지 않음)
Bellman Expectation Equation과 Bellman Optimal Equtaion이 다른 점
- max가 없으면 식을 넘길 수 있지만, 그렇지 않기 때문에 식 전개가 불가능
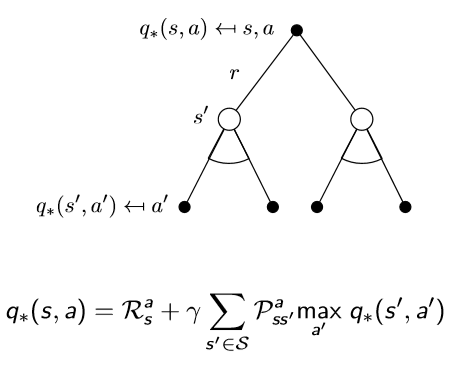

Bellman Optimally Equation이 MDP에서 성립하는지 간단하게 확인
6 = max { -2 + 8, -1 + 6}

Bellman Optimality Equation은 non-linear하기 때문에 closed form solution이 없다.
따라 여러 방법적인 value iteration, policy iteration, Q-learning, Sarsa 와 같은 solution들이 존재한다.
뒷 강의에는 위에 제시한 다양한 방법론들을 통해 MDP에서의 Optimally Policy를 찾아볼 예정이다.
아래는 교재 및 참고 블로그, 유튜브 강좌입니다.
deepmind.com/learning-resources/-introduction-reinforcement-learning-david-silver
Interested in learning more about reinforcement learning? Follow along in this video series as DeepMind Principal Scientist, cre
We research and build safe AI systems that learn how to solve problems and advance scientific discovery for all. Explore our work: deepmind.com/research
deepmind.com
www.youtube.com/watch?v=NMesGSXr8H4&list=LL&index=1&t=2178s
'논문 리뷰 > RL' 카테고리의 다른 글
| Lecture 6: Value Function Approximation (0) | 2021.01.19 |
|---|---|
| Lecture 5: Model-Free Control (0) | 2021.01.18 |
| Lecture 4: Model-Free Prediction (0) | 2021.01.15 |
| Lecture 3: Planning by Dynamic Programming (0) | 2021.01.13 |
| Lecture 2: Markov Decision Processes (1) (0) | 2021.01.05 |
| Lecture 1: Introduction to Reinforcement Learning (0) | 2021.01.04 |




댓글