Planning: env에 대한 model이 있을 때(model-based), 더 나은 policy를 찾아나가는 과정
Dynamic Programming: Planning 기법 중 한 가지

이번 목차에서 배울 용어 정리
Policy Evaluation(평가): policy가 정해졌을 때, MDP에서 policy를 따라가면서 value fn를 찾는 것
Policy Iteration, Value Iteration: policy/value 기반의 최적 방식을 찾는 것
강화학습에 국한된 것이 아닌 일반적인 DP의 특성

- 복잡한 문제를 푸는 방법론: 큰 문제를 sub 문제로 분할하고, 분할한 문제들의 솔루션을 찾고 모으는 방식으로 해결

model-free: env가 어떤지 모르는 상황, 완전한 정보가 없을 때
model-based: env에 대한 model이 있고, 모든 상황을 알 경우
Planning에서의 Dynamic Programming 방식은 model-based 환경에서 진행된다.
- DP가 되기 위해서는 두가지 조건이 필요하다.
- Optimal substructure: 전체 문제에 대한 optimal solution이 작은 문제들로 나뉠 수 있어야한다.
- Overlapping subproblems: 한 sub 문제를 풀어서 cached하고 재사용 가능하다.
- MDP가 이 두 조건에 완벽히 적합하다.
MDP에 DP를 적용 가능하다. ex) Bellman 방정식이 recursive하게 subproblem들로 나뉘어짐

- DP는 MDP의 모든 지식을 알고 있다고 가정한다. state transition, probability...
- DP가 Planning에 쓰인다.
- Prediction: value fn를 학습하는 것,
input: MDP + policy => output: policy를 따랐을 때의 value fn ex) Policy Evalutation
- Control: optimal policy를 찾는 것
input: MDP =>output: optimal policy 탐색 ex) Policy Iteration, Value Iteration

- DP는 RL이 아니어도 다양한 문제들에서 쓰인다.

- Problem: policy 를 진행했을 때, return 값이 얼마인지를 알게 되는 것 = value fn(Prediction 문제)
- Solution: Bellman expectation backup을 반복하는 방식이다.
V1(모든 value fn = 0) => V2(update) => ... => Vpi
- Using synchronous backups(잠깐 메모리에 저장하는 것 cached)
- s' = s에서 갈수 있는 state
모든 state를 Bellman expectation equation를 이용해서 칸에 있는 모든 값을 update
== 다음 state의 value 값들을 이용해서 iterative하게 update
- 계속해서 update하여 iteration 시, Vpi에 수렴하게 된다.
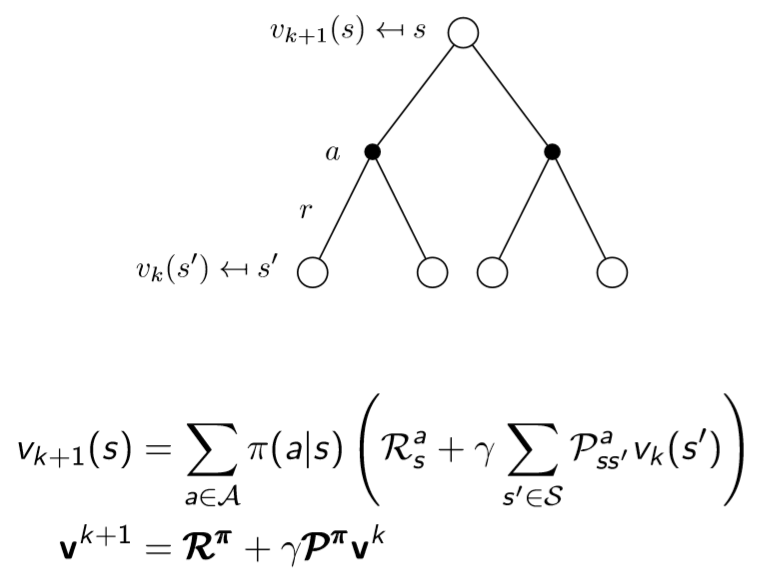
Policy Evaluation: 최상단의 value fn를 정확하게 하기 위해, 갈 수 있는 다음 4개의 s'의 값을 이용해서 s값을 다음 action들의 정확한 reward로 update 시킴
여기서 Bellman expectation equation 사용

Prediction Problem : MDP + Policy가 주어져야함
- discount factor r=1인, MDP episode
- 14 state + 1 terminal state
- grid를 벗어나는 state transition의 경우에는 그대로 위치
- reward가 1번 움직일 때마다 -1
- 각 state마다 1/4 확률의 random policy
pi(north, east, south, west) = 0.25
value fn는 결국 random policy를 따라 reward를 얼마나 받느냐 계산

state칸 만큼 table를 만들어 두고 0으로 초기화
이론적으로 어떻게 초기화하던 true value fn로 도달 = 좋은 초기화가 있을 수도 있지만 현실적으로 어려움
k번 iterative할 때마다 value fn이 update화 됨
[update 과정]
next iteration 모든 칸에 reward -1를 먼저 받고, 도착한 곳의 value fn이 쓰임
terminal에서는 action이 끝났으므로 0 고정, r = 1로 계산
k=1의 (1, 1) state [-1]: 0.25 * (-1) + 0.25 * (-1) + 0.25 * (-1) + 0.25 * (-1) = -1
k=2의 (1, 0) state [-1.75]: 0.25 * (-1) + 0.25 * (-2) + 0.25 * (-2) + 0.25 * (-2) = -1.75
과정을 반복하면 최적 policy에 도달

David silver: 어떤 주어진 (바보같은) random policy로 평가만 했을 뿐인데, 평가한 value fn를 가지고 greedy하게 움직이면 optimal policy를 찾는 것이 가능하다. == Policy Evaluation
무한히 갈 필요가 없어도 최적 policy를 찾을 수 있음

주어진 policy pi로
- policy evaluate: value fn를 찾는 것
- policy improve: greedy value fn를 찾아 움직이는 새로운 policy 생성
더 많은 iteration/evaluation를 통한 향상을 통해, optimal policy에 도달

- Policy evaluation: 현 env에서의 value fn를 계산
- Policy improvement: 주어진 value fn를 통해 greedy policy 계산
evaluation => improvement => evaluation => improvement => ... 반복하면 optimal value fn, pi에 도달한다.
어떤 policy라도 evaluation과 improvement가 가능하다 == optimal policy에 도달할 수 있다
evaluation => improvment가 iterative하게 진행되어 value fn이 수렴되고, optimal policy생성 예시

- states: locations이 두 곳이고, 한곳에는 최대 20개의 차가 존재 가능
- actions: 밤마다 5개의 차를 옮겨야함
- reward: 한 차에 $10(가능하다면)
- transitions: 차 반납과 요청이 랜덤

x축은 B지점에 있는 차의 수, y축 A지점에 있는 차의 수
등고선에 써져있는 숫자 값들: A => B로 n개의 차를 옮기는 policy
pi0(차를 한대도 안옮기는 경우)부터 greedy 하게 움직이는 policy를 만들며 value fn를 update한다.
evaluation과 improvement 이후의 값 V4: x, y 에서의 value fn 값으로 수렴한다.

policy improve를 하면 정말로 더 나은 policy가 되는가? 에 대한 증명
- deterministic policy를 가정
- greedy하게 움직이게 하는 것으로 policy를 improve할 수 있다.
pi'(s) = argmax Qpi(s,a) 결국 pi' policy가 더 좋다
Qpi(s, pi'(s)) = max Qpi(s,a) >= Qpi(s, pi(s))= Vpi(s)
- Vpi(s): pi를 따라서 얻을 수 있는 value fn
- Qpi(s, pi(s)): pi를 진행했을 때의 action으로 얻을 수 있는 value fn
- max Qpi(s,a): s에서 할 수 있는 모든 a중에 가장 value fn이 높은 것 == greedy policy를 따랐을 때의 Qpi(s, pi'(s))
Bellman equation을 적용하여 Qpi(s, pi'(s)) = Vpi'(s)임을 증명
모든 state의 value fn이 pi'에서 pi보다 높다는 결론
첫 step에 pi'따라서 한 action을 하고, 이후에는 pi를 따라가는 value fn >= 처음부터 pi를 따라가는 value fn

improvement가 무한히 좋아지지는 않기 때문에, 어느 순간 멈추게 되면 등식이 성립
Qpi(s, pi'(s)) = max Qpi(s,a) = Qpi(s, pi(s))= Vpi(s)
- 그렇다면 Bellman optimality equation이 성립하게 된다.
- 그러므로 모든 state에 대해 Vpi(s) = optimal V*(s)
- pi는 optimal policy

- policy evaluation 단계에서 꼭 Vpi에 수렴을 해야하는가? k를 무한까지 iterative해야하나?
- 아니면 그 전에 iterative를 종료시켜야하나?
- 아니면 iterative policy evaluation을 k번까지만 돌려야하나?
- 예를 들어, small gridworld에서는 k=3에서 optimal policy에 충족했다.
- 왜 매 iteration마다 policy를 update하지 않는가? policy iteration k=1 상황 == 이는 value iteration과 동일하다.

optimal policy는 두가지요소로 구성
- 첫 action이 optimal하다.
- 그 action이후의 s'에 도달하면 거기서 부터 또 optimal policy를 찾아간다.
어떤 policy pi는 다음의 조건을 충족하면 optimal value를 achieve한다.
- if and only if(필요충분조건) s에서 도달가능한 모든 s'로부터 pi가 거기서부터 optimal value를 achieves하면

- sub problems로 나누어 문제해결이 가능하다.
- sub problems의 v*(s')의 solution 알면 one-step lookahead를 통해 v*(s) 해결이 가능
Bellman optimality equation: V*(s) = max {Ras + r ∑Pass'V*(s')}
- intuition: goal부터 시작하여 직전 step을 알아나가는 과정을 통해 minimum거리 계산이 가능
- loopy, stochastic MDP에서도 적용이 가능하다.
Policy Iteration: policy Evaluation, Improvement를 반복하였고, policy가 존재 / bellman expectation equation 사용(policy를 따랐을 때의 value fn이 어떻게 되나)
Value Iteration: 명시적인 policy없이 value만 사용해서 iterative하게 update(policy evaluation이 없다) / bellman optimality equation 사용

policy 가 없고 랜덤한 값으로 주어지고, 한 step들은 bellman optimality equation이 적용
small problem 경우 끝부터 해나가도 되지만, 현실에서는 terminal state 주변에 어떤게 있는지 알기 조차 어렵다.
모든 state를 step마다 synchronize하게 안 뒤에야 넘어갈 수 있다.
모든 테이블에 있는 값을 update
V*(s) = max {Ras + r ∑Pass'V*(s')}
V1: 임의의 값 0으로 모든 state 채워넣음
V2(0,2): -1(e), -1(n), -1(s)중에서 max = -1
V3(1,0): -2(e), -2(s), 0(terminal) 중에서 max = -1 + 0 = -1
terminal에 가까운 값부터 확정이 되는 모습 관찰 가능
모든 state의 value를 구할 수 있고, policy 또한 계산 가능

- problem: optimal policy를 찾는다.
- solution: Bellman optimality backup을 iterative하게 적용한다.
- synchronous backsups를 사용한다.
각 iteration마다 모든 state에 대해 Vk(s')을 이용하여 Vk+1(s)를 update
- V*로 convergence하는 것은 추후에 증명
- policy itreation과 다르게 explicit한 policy가 없다.
- 중간 value fn는 어떤 policy의 value도 아니다.
이 위에서 greedy policy 적용이 가능하다.

Bellman optimality equation: max가 들어가는 bellman equation

오늘 내용 총정리 table
Synchronous: on-step에 모든 states들을 update하는 방식
Prediction: Bellman Expectation Equation을 반복 적용하는 방식
full-Width: 모든 state를 돌아가면서 한번 update를 하는 것
- state-value fn 기반의 알고리즘은 complexity가 m개 action, n개 state일 때 mn^2 시간 복잡도를 지닌다.
- action-value fn 기반의 알고리즘은 complexity가 " "일 때 m^2n^2 시간복잡도를 지닌다.
Extenstions to DP

- DP는 모든 states가 parallel하게 backup되는 synchronous 방식을 사용한다.
- 그러나 어떤 states만 update 한다던지, 순서를 다르게 하는 asynchronous DP도 존재한다.
- asynchronous 방식을 사용하면 computation 시간을 줄일 수 있고, 모든 states가 언젠간 모두 선택된다는 가정 하에converging함을 보장 가능하다.


실제로 코딩을 하기 위해서 두번째 table을 update하기 위해서는 첫번째 table의 값을 사용해야함
In-place: 1개의 Array만 사용하여 값을 계속 최신화

Prioritised Sweeping: state별 value update에 우선순위를 둠
bellman error: 두 table의 값의 차이가 클수록 중요하다고 간주

Real-Time DP: state가 굉장이 많고 agent가 가는 것은 한정적일 때(결국에는 다 방문하긴 해야함), agent를 움직이게 해놓고 방문한 state를 먼저 update <=> 지금까지는 agent없이 모든 state를 update

- DP는 Full-Width backup을 사용한다.
- synchro던 asynchro던 successor(s') state와 action이 고려된다.
- DP는 mideum-sized problems에서 효과적이다.
- 큰 문제에서는 너무 많은 state를 고려해야하므로 불가능하다.
- state의 개수가 늘어날 수록 expotentially하게 시간복잡도가 커지므로, one backup이 너무 비싸진다.
결론: 비효율적인 full-width backups

장점
- state가 많아져도 가격이 싸다.
- model-free(내가 action을 해도 어디에 도착할지도 모름) 상황에서도 사용 가능하다.
아래는 교재 및 참고 블로그, 유튜브 강좌입니다.
deepmind.com/learning-resources/-introduction-reinforcement-learning-david-silver
Interested in learning more about reinforcement learning? Follow along in this video series as DeepMind Principal Scientist, cre
We research and build safe AI systems that learn how to solve problems and advance scientific discovery for all. Explore our work: deepmind.com/research
deepmind.com
www.youtube.com/watch?v=rrTxOkbHj-M&list=LL&index=2&t=3s
'논문 리뷰 > RL' 카테고리의 다른 글
| Lecture 6: Value Function Approximation (0) | 2021.01.19 |
|---|---|
| Lecture 5: Model-Free Control (0) | 2021.01.18 |
| Lecture 4: Model-Free Prediction (0) | 2021.01.15 |
| Lecture 2: Markov Decision Processes (2) (0) | 2021.01.05 |
| Lecture 2: Markov Decision Processes (1) (0) | 2021.01.05 |
| Lecture 1: Introduction to Reinforcement Learning (0) | 2021.01.04 |




댓글