Deep Reinforcement Learning Hands-On - Maxim Lapan 교재 Chapter 09를 참고하였습니다.
remind action Value func definition Q(s,a).
Q-learning(DQN)에서의 중심 토픽은 action value func:Q(St, At)었다.
이 때, Q(s,a)는 bellman equation에 따라 다음과 같이 정의된다.
- Bellman Equation: Q(s,a)는 (current reward)Rt+1 + (discounted vector)r * Q(St+1, At+1) 로 분해된다.

- Q(s,a): s에서 a한 current reward+r*{Σ (s'이 될 확률) * (s'에서의 value)}
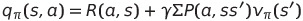
difference with Q-learning and PG?
if 모든 value를 알고 있다면, greedy-value하게 움직이기만 해도 episode 끝에 good total reward에 수렴한다. 자연스럽게 Value Iteration method의 state마다의 value나 Q-learning의 state+action은 best reward를 향한다. 우리는 여기서 action의 value를 찾기 위해 methods에서 위의 bellman equation을 사용하였다.
이때 agent는 state에서 어떤 행동을 해야하는지에 대해 정의한 policy에 따라 움직인다고 정의했다.
Q-learning에서는 value가 어떻게 움직여야 하는지 알려주었고, 이는 사실상 greedy-policy를 의미했다.
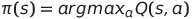
- π(s): policy π로 every state s에서 largest Q로 action
이러한 value-based method에서 탈출하여 policy-based한 방식이 바로 policy gradient이다.
Then why we have to use Policy Gradient?
1. RL problem을 해결할 때 우리가 찾고자 하는 것이 결국 policy이다.
: observation이 관찰 결과를 얻고 다음 해야할 일에 대한 결정을 내릴 필요가 있을 때 우리는 결국 value가 아닌 policy가 필요하다. 우리는 총 보상인 return에 관심이 있을 뿐, 모든 state에서의 정확한 value에 관심이 없다.
왜냐하면, 우리가 행동을 결정하기 전에 모든 value에 대해 계산하는 것은 어리석은 방식이기 때문이다. 결국 우리는 좀 더 빠른 결정을 내리기 위해, Q-learning에서의 value를 근사화하고 optimal한 action을 선택하는 것보다는 value를 신경쓰지 않고, 진행하는 것이 추가작업이 필요없는 효율적인 대안이다.
2. action이 무수하게 많은 환경이나, continues한 action space(예로 0~1사이 실수의 action)의 경우가 있기 때문이다.
: Q(s,a)를 최대화 하기 위해서는 a를 찾기 위해 너무 많은 small optimization 문제를 풀어야한다. action이 간단하지 않을 경우에는 최적화 문제가 상당히 어려워진다. Q는 일반적으로 매우 비선형적인 NN으로 표현되기 때문에, 최대화하는 인수를 찾는 것이 까다롭다. 따라서 value를 피하고 policy를 직접 찾는 것이 훨씬 효율적일 수 있다.
3. deterministic이 아닌 stochastic policy(확률성 action)을 배울 수 있다.
: policy 학습에 적합한 환경은 stochastic한 환경이다. policy는 자연스럽게 action 확률로 표현되며 이는 categorical DQN 방법과 동일한 방향성을 가진다고 한다.
How to represent Policy?
우리는 네트워크가 action를 parameterize하기를 원하도록 하려면 몇가지 옵션이 있다.
- deterministic action: action의 identifier를 반환한다.
- stochastic action: action의 확률 분포를 return. (분류 모델과 같은 일반적인 경우) 다른 말로, N개의 상호 배타적인 action에 대해, 각 action을 수행할 확률을 나타내는 N개의 숫자를 반환한다.
이산 숫자로 출력할 경우에는 가중치가 조금만 수정되어도 다른 action으로 표현될 수 있다. 그러나 출력이 확률 분포인 경우 가중치의 작은 변화는 출력에 큰 영향을 미치지 않는다. gradient optimization method는 결과를 개선하기위해 모델의 매개변수를 약간 조정하기 때문에 이 또한 적합하다.
Policy Gradient 수학적 개념 보충 설명 추가
T아카데미 [토크ON세미나] 강의 참고
www.youtube.com/watch?v=DgSROzUJmLw&list=PL9mhQYIlKEhc-n4vu4cWChTaNMi0mwYn4&index=3
NN을 이용한 Policy의 파라미터를 θ(vector)라고 설정하고 표현하면 Policy를 다음과 같이 표현할 수 있다.
- s가 주어졌을 때, a의 확률을 내뱉는 policy:

목적: πθ(policy)의 성능을 나타내는 함수 U(θ)에 대한 gradient를 구해서 πθ를 update하면 된다.
- [πθ를 따랐을 때 reward의 총합]의 기댓값(Expectation):

# reward의 총합(return)은 policy 실행시마다 매번 다르기 때문에 Expectation을 사용
우리의 목적은 U(θ)의 증가이므로 gradient U(θ)가 필요 => but 미분하기 위해서 기댓값 연산자를 없애야 함
episode의 Trasactory τ: s0, a0, s1, a1, s2, a2 ... sτ, aτ # s0만 같고 뒤부터는 매번 다름
- τ에서 발생한 reward의 합을 다음과 같이 정의하면
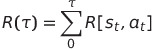
U(θ)는 다음과 같이 Expectation: (τ 발생확률)*(τ reward)로 풀어서 쓸 수 있다.

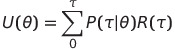
이제 U(θ)를 미분하게 되면 다음과 같은 식이 나오게 된다.

수학적 변환을 자세히 다루지는 않겠지만 변형이 이루어지고 다음과 같은 꼴을 이룬다.
- 모든 trasactory τ에 대한 Σ합:

# 값 * 확률 = 값의 기댓값이므로 Σ는 Expectation으로 표현된다.

이 Gradient 값을 통해 우리가 알 수 있는 것은 뭘까?
if R(τ)>0: 그 경로의 로그확률을 증가 == 어떤 τ reward가 좋았으면 로그의 발생확률을 증가시켜라
if R(τ)<0: 그 경로의 로그확률을 감소 == 위와 반대의 표현으로, 확률을 감소 시키는 방향으로 update해라
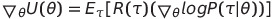
결국 gradientθ U(θ)를 구하는 것은 R(t) gradientθ logP(t|θ)를 batch size만큼 구한 평균값과 같다.
현재 이 상태에서 이제 다시 τ를 제거해주는 수학적 변환을 거치게 되면 성능함수 U(θ)의 gradient는 다음과 같다.
# Gt: τ의 처음부터 끝까지의 reward의 합

수식 전환을 통해 몇가지 정리를 해보면
Policy Gradient는 결국 Policy를 미분하면 되는 것인가?
: gradient는 목적 함수 U(θ)에 대한 미분이다. 이전까지는 loss function을 minimize하기 위해 loss function에 대한 gradient를 구했지만 이번에는 θ가 주어졌을 때 θ로부터 정의되는 성능함수인 U(θ)를 정의하였다.
gradient를 구해서 step size a만큼 빼주면 되는가?
: 우리는 maximize를 원하므로 더해주어야 한다. 면밀히 말하면 gradient ascent.
결국 gradientθ U(θ)인 식에서 기댓값 Eτ는 어떻게 계산하는가?
: τ에 대한 기댓값이기 때문에 Sample Mean(batch size 평균값)을 이용한다.

1. τ를 m개 돌려서 m개의 episode를 쌓고, (one sample도 상관없다)
2. 각 episode의 처음부터 끝까지 gradient log pi * Gt를 계산해서 모두 더해준 뒤
3. m으로 나눈다.
그것으로 U(θ)를 update 해주면 된다. 이것이 REINFORCE method이다.
이때 Gt는 뒤로부터 계산하는 것이 유리하다.
if, reward가 [r1, r2, r3 ... r100]까지 있다고 할 때,
G100 = R = r100 + γ*0
G99 = r99 + γ*r100
G98 = r98 + γ(r99 + γ^2(r100))
==γ*(r99)
진짜 마지막으로 정리해보자면
우리가 위 식에서 구해야 하는 것?

누구를 미분하면 위의 식이 되는가?
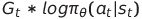
그러면 loss는 어떻게?

-는 왜 붙지?
: loss는 자동으로 minimize 시키는데 우리는 maximize하고 싶으니까(gradient ascent)
PG 표현 방식과 REINFORCE method?
교재에서의 REINFORCE 정의 방식에 대해 다시 살펴보겠다. 위의 몇 가지 수학적 표기법을 살펴볼 필요가 있다
- PG를 다음의 식으로 정의

: PG는 네트워크 매개 변수를 변경해야하는 방향(policy를 향상 시키는 방향)을 정의한다. 누적된 총 보상인 return을 계산하여 policy를 개선한다. gradient의 크기는 행한 action의 value에 비례하며, 직관적으로 이것은 우리에게 좋은 return을 제공한 행동의 확률을 높이는 것을 의미한다.
E expectation 환경에서 PG는 누적 된 총 보상 측면에서 정책을 개선하기 위해 네트워크 매개 변수를 변경해야하는 방향을 정의한다. gradient의 척도는 취해진 action의 값에 비례하며, 이는 위 공식에서 Q (s, a)이며 기울기 자체는 취해진 조치의 로그 확률의 gradient와 같다.
# REINFORCE에서는 MC 방식이므로 Gt(return)을 사용하긴하는데.. 교재에선 one-step을 기준으로 말한 것 같음..?
직관적으로 이것은 우리에게 좋은 총 보상을 제공 한 행동의 확률을 높이고 최종 결과가 좋지 않은 행동의 확률을 낮추려고한다는 것을 의미한다.
공식에서 E expectation 값은 환경에서 수행 한 여러 단계를 수행하고 gradient를 평균화한다는 것을 의미합니다. 실용적인 관점에서 PG 방법은 L = −Q (s, a) logπ (a | s)와 같은 손실 함수의 최적화를 수행하는 것으로 구현 될 수 있다. SGD (Stochastic Gradient Descent) 중에 손실 함수가 최소화되므로 빼기 대신 더해주어 정책 기울기를 최대화한다.
Q(s,a)를 PG 훈련에 사용하는 것이 분명한 개선이 있을 것이다. 왜냐하면 episode들을 세밀하게 분리하였기 때문이다.
예를 들어, ttl reward = 10인 epidode의 return은 ttl reward = 1인 episode의 return보다 기울기에 더 많이 관여된다.
- idea: episode 시작 부분에 좋은 행동의 확률을 높이고, epidode 끝 부분에 가까운 행동을 줄인다.
방법은 다음과 같다.
- Initialize the network with random weights
: 무작위 가중치로 네트워크 초기화 - Play N full episodes, saving their (s, a, r, s’) transitions
: N개의 전체 episode 재생, (s, a, r, s') trasactory 저장 - For every step t of every episode k, calculate the discounted total reward for subsequent steps Qk,t = i=0 γiri : 모든 episode k의 모든 단계 t에 대한 후속 단계에 대해 discount된 총 보상을 계산한다.
- Calculate the loss function for all transitions L = − k,t Qk,t log(π(sk,t, ak,t))
: 모든 transition에 대한 손실 함수를 계산한다. - Perform SGD update of weights minimizing the loss
: 손실을 최소화하는 가중치의 SGD 업데이트를 수행한다. - Repeat from step 2 until converged
: 수렴될 때까지 2단계부터 반복합니다.
위의 알고리즘은 몇 가지 중요한 측면에서 Q- 러닝과 다르다.
- 명시적인 탐색이 필요하지 않습니다.
: Q-learning에서 우리는 e-greedy 전략을 사용하여 환경을 탐색하고 에이전트가 최적이 아닌 정책에 갇히지 않도록 방지했습니다. 이제 네트워크에서 반환 된 확률로 탐색이 자동으로 수행됩니다. 처음에 네트워크는 무작위 가중치로 초기화되고 네트워크는 균일 한 확률 분포를 반환합니다. 이 분포는 임의의 에이전트 동작에 해당합니다.
- replay 버퍼가 사용되지 않습니다.
: PG 메서드는 on-policy 메서드 클래스에 속하므로 이전 정책에서 가져온 데이터를 학습 할 수 없다. 좋은 점은 이러한 방법이 일반적으로 더 빨리 수렴된다는 것이다. 단점은 일반적으로 DQN과 같은 정책을 벗어난 방법보다 환경과 훨씬 더 많은 상호 작용이 필요하다는 것이다.
- 대상 네트워크가 필요하지 않습니다.
: 여기서 우리는 Q-value를 사용하지만 환경에서의 경험에서 얻은 것입니다. DQN에서는 대상 네트워크를 사용하여 Q- 값 근사에서 상관 관계를 끊었지만 더 이상 근사하지 않습니다. 나중에 대상 네트워크 트릭이 PG 방법에서 여전히 유용 할 수 있음을 알 수 있습니다.
import gym
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torch.distributions import Categorical
#Hyperparameters
learning_rate = 0.0002
gamma = 0.98 # 무조건 끝나는 episode라면 gamma == 1도 가능하다.
class Policy(nn.Module):
def __init__(self):
super(Policy, self).__init__()
self.data = []
# weight를 정의
self.fc1 = nn.Linear(4, 128) # fully connected first layer
self.fc2 = nn.Linear(128, 2) # fully connected second layer
self.optimizer = optim.Adam(self.parameters(), lr=learning_rate)
def forward(self, x):
x = F.relu(self.fc1(x)) # first layer 통과 후 비선형 함수 통과
x = F.softmax(self.fc2(x), dim=0) # second layer 통과 후 sofrmax로 합이 1이 되는 확률로 만들어
return x
# s, a pair 저장
def put_data(self, item):
self.data.append(item)
def train_net(self):
R = 0
self.optimizer.zero_grad()
for r, prob in self.data[::-1]: # return을 재귀적으로 뒤에서부터 더하면서 계산
R = r + gamma * R # Return Gt
loss = -torch.log(prob) * R # loss function
loss.backward() # gradient 계산
self.optimizer.step() # Adam optimizer update 진해
self.data = []
# main role: 경험을 쌓는 역할
def main():
env = gym.make('CartPole-v1')
pi = Policy()
score = 0.0
print_interval = 20
for n_epi in range(10000):
s = env.reset() # env 초기화 상태를 받은 numpy 배열 n
done = False
while not done: # CartPole-v1 forced to terminates at 500 step. # Cartpole이 500번 성공하면 보통 성공이라고 봄
prob = pi(torch.from_numpy(s).float()) # Pi에 (numpy 배열을 pytorch로 바꾼) state를 넣으면 각 action들의 확률이 리턴 Tensor(0.0255, -0.0159, -0.04898, -0.0408)
m = Categorical(prob) # prob 중 높은 확률 값을 리턴
a = m.sample() # 이러한 확률을 가진 action에서 직접 sampling하면 cartpole의 경우에는 action이 0 아니면 1 두가지중 하나로 나옴 Tensor(0)
s_prime, r, done, info = env.step(a.item()) # 그 action을 env.step에 넣어주면 다음 상태, 보상, 겜 종료 여부를 받는다.
pi.put_data((r,prob[a])) # policy 객체에 학습에 써야하기 때문에 reward, 내가 선택한 action인 prob[a] 확률을 모은다. # 내가 선택하지 않은 action의 확률인 prob 쓰이지 않는다.
s = s_prime # next state
score += r
pi.train_net()
if n_epi%print_interval==0 and n_epi!=0:
print("# of episode :{}, avg score : {}".format(n_epi, score/print_interval))
score = 0.0
env.close()
if __name__ == '__main__':
main()
Then, which is more effective for DQN and PG in the above environment?
: REINFORCE는 DQN보다 더 빠르게 수렴되며, CartPole env를 해결하는데 필요한 step과 episode #을 줄여준다.
DQN 방식은 Cartpole env를 해결하기 위해 각각 16부작 40개 정도의 batches가 필요했는데, 총 640batches. REINFORCE 방식은 300회 미만의 에피소드에서도 동일한 작업을 수행할 수 있어 좋은 개선점이 될 수 있다.

Policy-based versus value-based methods?
- Policy methods
policy는 우리가 관심을 갖는 것: 우리의 behavior를 직접적으로 최적화 하는 것이다.
on-Policy 방식이며, 환경으로부터 새 sample를 필요로 한다.
Policy methods는 sample-efficient가 떨어지기 때문에 환경과의 상호작용이 더 많이 요구된다.
위의 예시에서 우리는 training 도중 action probability를 얻기 위해 NN에 오직 한번 접근하게 된다.
- Value method
DQN과 같이, 간접적으롣 동일한 방법을 사행하여 먼저 value를 학습하고 이 값을 기반으로 policy 제공
old policy, human demonstration, other sources가 포함된 old data로부터 이익을 추구한다.
large replay buffer의 이점을 활용 가능하다.
sample-efficient가 더 높다는 것은 value method가 계산적으로 더 효율적이라는 것을 의미하지는 않는다.
DQN에서는 Bellman update에서의 next state와 current state의 두가지 state batch를 처리해야 한다.
두 방법 중 한쪽에 대한 월등한 이점은 보이지 않는 것을 알 수 있다.
실제로 continuous control problem, access to env is cheap and fast와 같은 상황에 대해서는 Policy method가 더 자연스러운 선택이 될 수 있다.
그러나 Value method가 빛을 바라는 많은 상황들이 존재한다. DQN variants가 달성한 Atari game의 결과가 그렇다.
이상적으로 우리는 양쪽 방식에 대해 모두 친숙하고 양쪽 방식의 강하고 약한면을 이해해야 한다.
Limitations of REINFORCE methods?
- Full episodes are required
: training에서 우리는 full episode가 끝날때까지 기다려야만 한다.
: more episodes는 more training을 의미하고 이는 곧 more accurate PG를 의미하므로 REINFORCE는 많은 episode를 필요로 한다. 이는 CartPole과 같은 쉬운 example에서는 10 step이 넘어가도 괜찮지만, Pong에서는 완전히 다르다: every episode가 100을 넘어 1000 frames까지 진행된다. 이는 training 관점에서 매우 나쁘다. training batch가 점점 커지고, low sample efficiency로 인해, single training step을 위해 많은 env와의 communicate가 필요한 경우이다.
complete episode 요구사항의 본질은 정확한 Q estimation을 얻는 것이다. DQN에서 우리는 one-step Bellman equation을 사용하여 exact value를 estimation discounted reward로 대체 가능했다.

V(s)를 추측하기 위해서 우리는 Q-estimation을 이용했는데, PG에는 V(s) or Q(s,a)가 없다.
이를 극복하기 위해서, 2가지 접근 방법이 존재한다.
1. 네트워크에 V(s)를 추정하도록 요청하고 이 estimation을 이용하여 Q를 얻는다: A2C method (next chapter)
2. N step 앞에 있는 Bellman equation를 풀 수 있다.
: gamma가 1미만일때 value에 대한 contribution이 감소하고 있다는 사실을 효과적으로 사용할 수 있다. 실제로 gamma=0.9일때 10-step뒤의 value coefficient는 0.35, 50-step뒤의 coefficient는 0.00515로 reward에 대한 기여도가 매우 작은 것을 볼 수 있다. gamma=0.99이면, 요구되는 step이 더 커지지만 가능은 하다.
- High gradients variance
: PG formula J()에서 우리는 주어진 state에서의 discounted reward에 비례하는 gradient를 가진다. 그러나 reward의 range는 env에 크게 의존적이다.
예를 들어, Cartpole환경에서 폴을 수직으로 잡을 때마다 1의 reward를 받는다고 했을 때, 5의 reward를 받는 episode와 100의 reward를 받는 episode가 존재할 수 있다. 이는 성공적이지 않은 샘플의 gradient가 더 성공적인 샘플의 gradient보다 20배 더 낮다는 것을 의미하게 된다.
이러한 큰 차이는 final gradient에서 하나의 운좋은 episode가 지배할 것이기 때문에, training에 큰 영향을 미칠 수 있다.
수학적으로 PG는 high variance를 가지고 있고, 우리는 복잡한 환경에서 이것에 대해 따로 무언가를 할 필요가 있다. 그렇지 않으면 training process가 불안정해질 수 있다.
이를 처리하기 위한 일반적인 방법으로는 Q에서 baseline(기준선)을 빼주는 것이다. baseline의 가능한 선택지는 다음과 같다.
1. 일반적인 discounted reward의 평균인 일정 값
2. discounted reward의 이동 평균
3. state의 value인 V(s)
- Exploration
: policy가 확률 분포로 표현되더라도, agent가 locally-optimal policy로 수렴하고 exploring을 중단할 가능성이 있다.
DQN에서는 e-greedy action choice(agent가 current policy에 의해 선택된 action대신 일부 무작위 action을 선택하는 방식)을 통해서 이 문제를 해결했다. 우리는 같은 접근법을 사용할 수 있지만, PG는 entropy bonus라는 더 나은 방식을 사용해 exploration을 진행한다.
정보 이론에서, entropy는 어떤 시스템의 불확실성의 척도이다. agent에 적용되는 entropy는 agent가 수행할 작업에
대해 불확실한 정도를 표시한다. 엔트로피 값은 항상 0보다 크고 정책이 동일할 대 단일 최대값을 가진다.
- entropy of policy H(pi)

즉, 모든 action probability는 동일하다. agent가 local minumum에 고착되지 않도록, 우리는 loss function에서 entropy를 빼서 agent가 취해야할 action에 대해 너무 확신을 갖지 못하게 처벌한다.
Correlation between samples problem
one single episode의 training smaples는 대개 크게 연관되어 SGD training에 좋지 않다.
DQN의 경우, training batch를 샘플링한 100k-1M 관측치를 가진 대형 replay buffer를 사용하여 이 문제를 해결했다. 이러한 방법은 on-policy 클래스에 속하기 때문에 이 솔루션은 PG algorithms에 적용되지 않는다.
시사하는 바는 간단합니다.
이전 policy에 의해 생성된 이전 sample을 사용하여 current policy가 아닌 old policy에 대한 PG를 얻을 수 있다.
하지만 유감스럽게도 잘못된 해결책은 replay buffer 크기를 줄이는 것이다. 몇 가지 간단한 경우에 효과가 있을 수 있지만, 일반적으로 현재 정책에 의해 생성된 새로운 training data가 필요하다.
이를 해결하기 위해 병렬 환경이 일반적으로 사용된다. 아이디어는 간단하다.
: 한 환경과 통신하는 대신 여러 환경을 사용하고 transition 과정을 training data로 사용한다.
vanila PG result
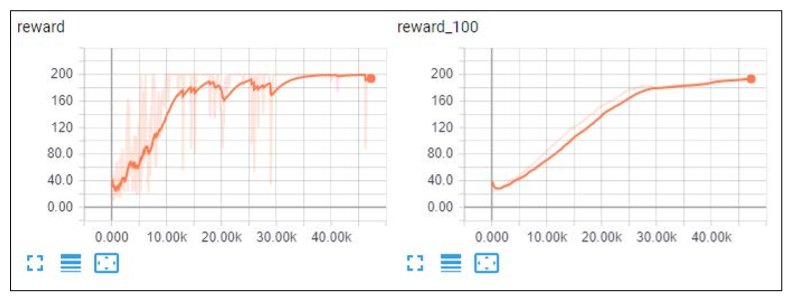
vanila PG와 REINFORCE 방식에서의 dynamics와 성능은 크게 다르지 않다.
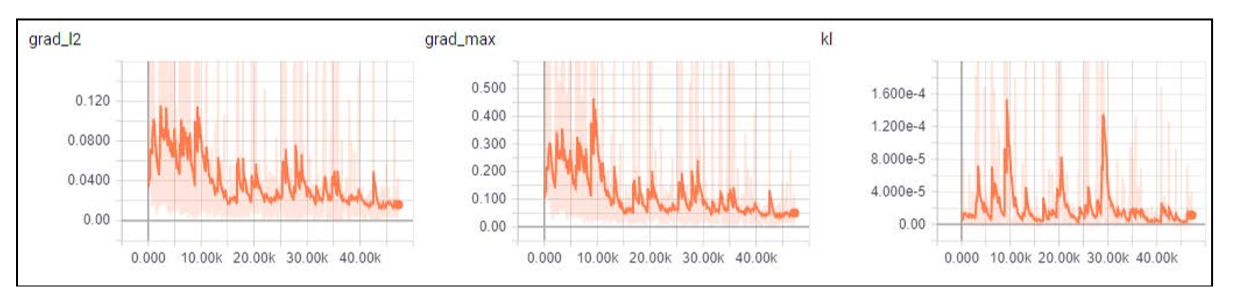
최종 차트는 gradient가 계속해서 수정되는 모습을 볼 수 있으며 크게 spike가 나타나는 것은 없다.
그러나 vanila PG는 더 복잡한 환경인 Atari Pong Game에서는 수렴에 실패하는 것을 보이는 불안정성을 가진다.
이러한 문제를 해결하기 위해 다음장의 A2C, A3C를 통해 수렴시킬 수 있다.
다음 장에서는 value-based 방법과 policy-based 방법을 모두 결합하여 PG의 안정성을 개선하는 방법을 검토한다.
'논문 리뷰 > RL' 카테고리의 다른 글
| 04. Dynamic Programming (0) | 2021.03.22 |
|---|---|
| 03. Finite Markov Decision Process (0) | 2021.03.20 |
| Vanila Actor-Critic (0) | 2021.03.09 |
| Lecture 7: Policy Gradient (0) | 2021.01.23 |
| Lecture 6: Value Function Approximation (0) | 2021.01.19 |
| Lecture 5: Model-Free Control (0) | 2021.01.18 |




댓글