Deep Reinforcement Learning Hands-On - Maxim Lapan 교재 Chapter 10를 참고하였습니다.
Variance reduction
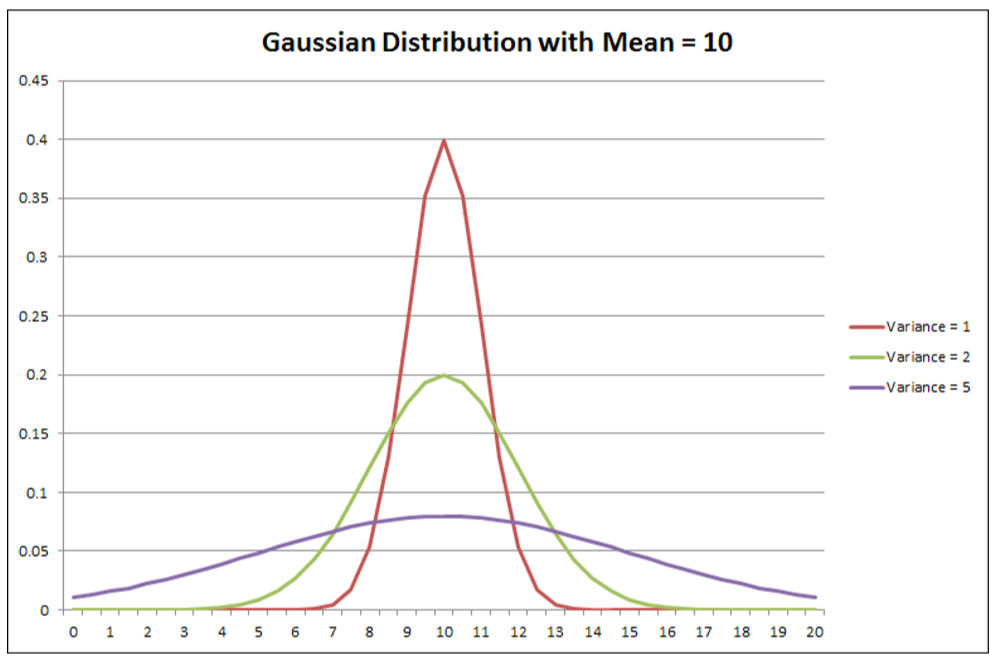
Policy Gradient method에서 안정성을 향상시키는 방법 중 하나가 gradient variance를 줄이는 것이라고 언급했었다. variance는 값이 평균으로부터 얼마나 멀리 분산되어 있는지를 보여준다. 만약 분산이 높다면 랜덤 변수가 평균에서 크게 벗어난 값을 취할 수 있다. 통계에서 분산은 다음과 같이 표현된다.
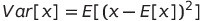
PG는 수학적으로 다음과 같이 정의되었었다.

vanila PG에서 Q(s, a)는 특정 상태에서 수행되는 action의 probability를 얼마나 증가 또는 감소시키는지 지정한다. REINFORCE에서는 discounted ttl reward(return)을 scaling에 사용했으므로 Q(s,a)가 아닌 Gt로 표현했었다.
REINFORCE의 안정성을 높이기 위해서 , gradient에서 mean reward(baseline)를 빼주었다.
따라 baseline이 있는 version의 variance가 없는 version보다 더 빨리 수렴한다.
Policy Gradient 수학적 개념 보충 설명 추가
T아카데미 [토크ON세미나] 강의 참고
www.youtube.com/watch?v=kRwVAVWt9c4&list=PL9mhQYIlKEhc-n4vu4cWChTaNMi0mwYn4&index=4
실제로 우리는 REINFORCE에서 특정 state에서 특정 action에 대한 적합성을 결정하기 위해 action의 discounted ttl reward를 사용하고 있었다. 그러나 ttl reward는 Q(s,a)의 expectation으로 표현이 가능하다.
- 기존 U(θ)

- 수학적 변환을 거친 U(θ) Gt의 기댓값이 Q로 표현

# Q: 어떤 state에서 action했을 때, 그 이후 return의 기댓값
[Q-A2C]: 실제 Q함수를 모르기 때문에 w 파라미터를 쓰는 또 다른 NN으로 표현

state S에 대한 임의의 함수 B(s)에 대해 다음의 식이 성립
# δ: state에 대한 점유도 함수, 특정 state는 자주 방문 당하면 δ의 확률이 높다 (Policy가 정해져야 정해지므로 policy에 따른 함수)



결국 state에 대한 어떤 함수가 와도 0이된다.
PG에서 B(s)를 빼줌으로써 variance를 감소시킬 수 있다.
Q-V를 하면 variance가 줄어든다는 것이 수학적으로 증명되어있음
평균보다 더 좋은 a는 더 하고, 안좋은 a는 안한다. 더 좋은 δ로 학습하겠다.
- Q-A2C - V(s), #Vπθ(s) = 0

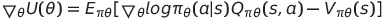

# Aπθ(s,a) = Qπθ(s,a)-Vπθ(s)
problem 너무 많은 파라미터가 필요
: θ, w, v 3개의 파라미터 필요


solution: TD error 사용
True Value function Vπθ(s)에 대한 TD error δπθ를 생각해보자

# δπθ: Aπθ(s,a)의 unbiased estimate, δπθ를 계속해서 평균낸 것이 Aπθ
따라 TD error = Aπθ의 sample이므로 TD error를 이용해 PG 계산이 가능하다.
실전에서는 Approximate TD error를 사용

이렇게 되면 state-value function V(s)만 학습하면 된다.
한마디로 baseline을 V(s)라고 생각하고 빼주는 것이다.
따라 PG의 U(θ)는 다음 논리를 거치면서 TD A2C가 가능해진다.

우리가 어떤 상태에 대한 값을 알고 있을 때(또는 적어도 그것에 대한 근사치를 가지고 있을 때) PG를 계산하고 정책 네트워크를 업데이트하여 장점 값이 좋은 행동에 대한 확률을 높이고 나쁜 이점을 가진 행동의 가능성을 줄일 수 있다. policy 네트워크(행동의 확률 분포를 반환하는)는 무엇을 해야 하는지를 지시하는 것처럼 Actor라고 불린다. 또 다른 네트워크는 Critic라고 불리는데, 그것은 우리의 행동이 얼마나 좋았는지 알려주기 때문이다.
이와 같은 구조를 Actor-Critic이라고 부른다.

training step
1. Initialize network parameters θ with random values
: 랜덤 값으로 네트워크 매개변수 θ 초기화
2. Play N steps in the environment using the current policy πθ, saving state st, action at, reward rt
: 현재 정책인 πθ를 사용하여 env에서 N단계를 실행하고 state , action, reward 저장
3. R = 0 if the end of the episode is reached or Vθ(st)
: 에피소드 끝에 도달한 경우나 Vθ(st)이면 R = 0
4. For { i = t -1 ... t start } (note that steps are processed backwards)
: 계산은 거꾸로 진행
- R <= ri + γR
- Accumulate the PG ∂θπ

- Accumulate the value gradient ∂θv

5. Update network parameters using the accumulated gradients, moving in the direction of PG ∂θπ and in the opposite direction of the value gradients ∂θv
: 누적 gradient를 사용하여 PG ∂θπ 방향으로, value gradient ∂θv의 반대 방향으로 네트워크 파라미터를 update
6. Repeat from step 2 until convergence is reached
: 2단계부터 수렴될 때까지 반복
import gym
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torch.distributions import Categorical
#Hyperparameters
learning_rate = 0.0002
gamma = 0.98
n_rollout = 10 # n-step하고 update할지
class ActorCritic(nn.Module):
def __init__(self):
super(ActorCritic, self).__init__()
self.data = []
self.fc1 = nn.Linear(4,256) # 공유되는 layer
self.fc_pi = nn.Linear(256,2)
self.fc_v = nn.Linear(256,1)
self.optimizer = optim.Adam(self.parameters(), lr=learning_rate)
# 두개의 NN
def pi(self, x, softmax_dim = 0): # pi NN
x = F.relu(self.fc1(x))
x = self.fc_pi(x)
prob = F.softmax(x, dim=softmax_dim) # softmax
return prob
def v(self, x): # value NN
x = F.relu(self.fc1(x))
v = self.fc_v(x) # value는 확률이 아니므로 softmax 불필요
return v
def put_data(self, transition):
self.data.append(transition)
# 모은 데이터로 batch를 생성
def make_batch(self):
s_lst, a_lst, r_lst, s_prime_lst, done_lst = [], [], [], [], []
for transition in self.data:
s,a,r,s_prime,done = transition
s_lst.append(s)
a_lst.append([a])
r_lst.append([r/100.0])
s_prime_lst.append(s_prime)
done_mask = 0.0 if done else 1.0
done_lst.append([done_mask])
# 같은 속성끼리 모아서 tensor로 전환
s_batch, a_batch, r_batch, s_prime_batch, done_batch = torch.tensor(s_lst, dtype=torch.float), torch.tensor(a_lst), \
torch.tensor(r_lst, dtype=torch.float), torch.tensor(s_prime_lst, dtype=torch.float), \
torch.tensor(done_lst, dtype=torch.float)
self.data = []
return s_batch, a_batch, r_batch, s_prime_batch, done_batch
# 학습 함수
def train_net(self):
s, a, r, s_prime, done = self.make_batch() # make_batch로 들어왔던 데이터 이용해서 tensor 생성됨
td_target = r + gamma * self.v(s_prime) * done # td_target: 정답
delta = td_target - self.v(s) # target - v(s)
pi = self.pi(s, softmax_dim=1) # pi action 확률들
pi_a = pi.gather(1,a) # 거기서 고른 action
loss = -torch.log(pi_a) * delta.detach() + F.smooth_l1_loss(self.v(s), td_target.detach())
#policy_loss # value_loss
# delta는 상수값이므로 detach() gradient가 생성되지 않게함
self.optimizer.zero_grad()
loss.mean().backward()
self.optimizer.step()
def main():
env = gym.make('CartPole-v1')
model = ActorCritic()
print_interval = 20
score = 0.0
for n_epi in range(10000):
done = False
s = env.reset()
while not done:
for t in range(n_rollout): # n_rollout만큼
prob = model.pi(torch.from_numpy(s).float()) # policy로 action 진행
m = Categorical(prob)
a = m.sample().item() # action 추출
s_prime, r, done, info = env.step(a) # 그 action을 env로 보내서 다음 s, a, r 추출
model.put_data((s,a,r,s_prime,done)) # s, a, r, s' 데이터 수집
s = s_prime
score += r
if done:
break
model.train_net()
if n_epi%print_interval==0 and n_epi!=0:
print("# of episode :{}, avg score : {:.1f}".format(n_epi, score/print_interval))
score = 0.0
env.close()
if __name__ == '__main__':
main()
'논문 리뷰 > RL' 카테고리의 다른 글
| DRQN (0) | 2021.03.25 |
|---|---|
| 04. Dynamic Programming (0) | 2021.03.22 |
| 03. Finite Markov Decision Process (0) | 2021.03.20 |
| REINFORCE(MC-PG) + vanila Policy Gradient (0) | 2021.03.04 |
| Lecture 7: Policy Gradient (0) | 2021.01.23 |
| Lecture 6: Value Function Approximation (0) | 2021.01.19 |




댓글