Dynamic Programming(DP): MDP 상태의 env에 대한 perfect model이 주어진 optimal policy를 계산하는 알고리즘의 집합이다.
DP는 너무 큰 computational cost 때문에 RL에서 limited utility로 쓰이지만, 추후에 다룰 method의 중요한 기초를 제공하므로 짚고 넘어간다. 다른 모든 methods들은 perfect env model에 대한 가정과 less computation만 제외하면 DP와 비슷한 효과를 내기위한 시도로 보일 수 있다.
우리는 env가 finite MDP라고 가정하였다.
DP가 continuous state, action spaces에 대한 문제에 활용되기는 하지만, 완벽한 solution은 특정 cases에서만 존재한다. 위 문제에 대한 approximate solution을 포함하는 일반적인 방법은 continuous state, action spaces를 양자화(이산)시킨 후에 finite-state DP methods를 적용하는 것이다.
RL에서 DP의 핵심 idea는 value function을 활용하여 good policy를 위한 구조를 searching 하는 것이다.
Bellman optimality equations 개념을 다시 사용한다.
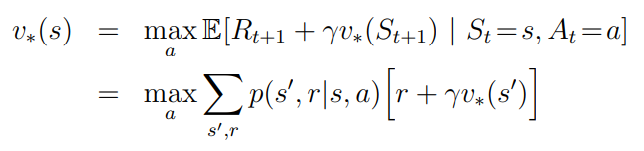
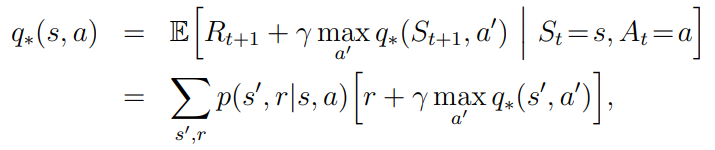
DP algorithms는 Bellman equation을 변환하여, 원하는 value function의 approximations를 개선하기 위한 update rule을 얻는다.
4.1 Policy Evaluation
Prediction problem: value function을 학습하는 것. MDP(complete env) + any policy가 제공; 전제조건
Iterative Policy Evaluation: 임시 policy π에서의 state-value function Vπ를 계산하는 방법

- 만약 env's dynamics가 completely known하다면, 위 마지막 방정식에서의 Vπ(s)는 linear equation이다.
approximate value function v0, v1, v2...의 sequence에서 initial value function v0가 임시로 정해졌다고 하자. 그리고 각각의 성공적인 approximation은 Vπ에 대한 Bellman equation을 update rule로 사용하여 얻어진다.
Vπ => Vk로 변경, 이 때 k가 무한으로 수렴하더라도 Vπ는여전히 보장된다.

Vk로부터 successive approximation인 Vk+1을 구하기 위해서는 각 state S에서 같은 operation을 수행한다.
full backs up
: DP에서는 가능한 모든 state를 기반으로 하여 backs up이 진행되므로 full backs up이라고 한다.
Iterative policy evaluation의 각 iteration에서는 모든 state에서 새로운 approximate value function Vk+1을 생성하기 위해 backs up을 진행한다.
Vk+1(s) = r + γ Vk(S')
- immediate reward는 현재 policy로 평가되는 one-step transition reward으로 설정
- current state S의 old value를 old value의 sucessor state S'로부터 오는 new value로 교체
To write a sequential computer program
- version(1) 2 arrays: old value; Vk(s), new value; Vk+1(s) 사용
: 두개의 array 사용. 변화없는 old value array로부터 new value가 계산된다.
- version(2) 1 arrays: 'in-place'; immediately value update
: new backed-up value가 즉시 old value를 overwriting 해버리기 때문에, 하나의 array를 사용하는 것이 당연히 더 쉽다.
그런 다음, state가 backup되는 order에 따라 오른쪽에 있는 old value 대신 새 값이 사용되는 경우가 있기도 하다.
'in-place' algorithm도 Vπ로 수렴하기는 한다. 실제로, 새 데이터를 사용할 수 있는 즉시 사용하기 때문에, 일반적으로 2 arrays version보다는 더 빠르게 수렴된다고 한다.
우리는 backups을 state space 전체에서 수행되는 것이라고 생각한다. (full backs up)
'in-place' algorithm의 경우 sweep 중에 state backup order는 수렴 속도에 중요한 영향을 미친다. 우리는 DP를 생각할 때 일반적으로 in-place version을 염두에 둔다.

공식적으로, Iterative policy evaluation은 limit 내에서 수렴되지만, 실제로는 시간이 지나면 중지되어야 한다.
일반적인 중지조건으로는 각 sweep 이후의 quantity; max|Vk+1(s) - Vk(S')| 를 측정하여 값이 충분히 작으면 종료한다.
4.2 Policy Improvement
Iterative policy evaluation 방법과 같이 value functinon을 계산하는 이유는 더 좋은 정책을 찾기 위해서이다.
우리는 임시 deterministic policy π로 value function Vπ를 정의하였다고 가정하고, value function을 통해 s에서 current policy가 얼마나 좋은지 알고있다.
- Problem: 몇몇 state에서, π로 deterministic하게 선택된 a를 바꿔야하는지 여부를 알고싶다.
- Solution: s에서의 a 선택을 고려한 뒤에 policy π를 결정한다.
- key criterion: value function size가 판단의 기준이 된다.
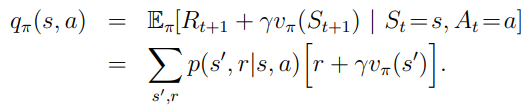
policy improvement theorem
- 모든 state 중 어떤 single state 대해 다음의 조건이 성립하면,

- expected return; Vπ가 모든 states에서 같거나 더 크고,
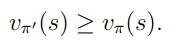
- changed policy π'는 무조건 π보다 좋다.
proof about π' is better than π

new greedy policy π'
given policy와 its value function이 주어진 경우, policy에서 single state의 particular action에서의 변화를 평가할 수 있고, 자연스럽게 확장시키면, all states에서의 all actions의 변화를 고려하여 best Qπ(s,a)를 선택이 가능하다.

greedy policy; π' : one-step lookahead에서 Vπ에서의 best action으로 행동한다.
구조적으로 policy improvement theorem을 만나게 되므로 우리는 original policy보다 더 좋은지에 대해 알 수 있다.
policy improvement: original policy의 value function을 greedy하게 만들어 improved new policy를 만드는 과정
만약 new greedy; policy π'가 original policy π와 같다고 하자.

이는 Bellman optimality equation과 같다는 것을 볼 수 있다.
- Vπ' = V*가 되고 π'와 π는 optimal policy이다.
따라서 Policy improvement는 original policy가 optimal한 경우를 제외하고는 훨씬 더 나은 policy를 제공해야 한다. policy improvement가 일어나지 않는 jam 상황이 발생하면 그것은 optimal policy라는 뜻이다.
how about stochastic policy?
현재까지는 deterministic policy에 대한 case만 살펴보았지만, general case의 경우에는 stochastic policy가 s에서 a의 확률인 π(a|s)를 구체화한다. 구체적인 detail은 뒤에서 살펴보고 위의 policy improvement theorem이 stochastic policy에도 충분히 확장가능하다는 것만 알아두면 된다.

게다가, maximum action을 선택한 상태에서 policy improvement jam이 발생하면, stochastic case에서는 actions들 중에 우리가 descrete하게 선택해야할 필요가 없다. 대신 각 maximizing action은 new greedy policy에서 선택될 확률로 표현된다. 모든 submaximal actions가 0이 아닌 이상 모든 확률이 선택 될 수 있다.
4.3 Policy Iteration
- Policy iteration: 단조롭게 improve되는 policy and value function의 sequence iteration
Policy π의 Vπ로 구한 better policy π'의 value function인 Vπ'를 구하고, greedy improve하고, improve한 policy를 생성하는 iteration을 반복하면서 optimal policy를 찾아나간다.
evaluation => improvement => evaluation => improvement => evaluation => improvement...

iteration은 policy evaluation의 수렴 속도를 크게 증가시킨다. (아마도 value function이 old policy에서 greedy policy로 크게 변하지 않기 때문이다. ) 또한 위 topology에서는 각 policy가 previous policy에 비해 엄격한 improve가 보장된다.

finite MDP에는 finite policies만 있기 때문에 이 process에서는 finite iteration에서 optimal policy와 optimal value function으로 수렴해야 한다.
grid world와 같은 example에서 policy iteration은 놀라울정도로 few iteration만으로 종종 수렴된다. 이런 경우에는 iteration을 진행할수록 better policy는 아니지만 optimal policy 상태이고, terminal states까지 최소한의 step으로 진행된다.
4.4 Value Iteration
policy iteration의 단점은 각 iteration에 policy evaluation이 포함되며 이는 그 자체로 여러번의 sweep을 필요로 하는(overhead가 매우 큰) computation일 수 있다. 또한 policy evaluation가 반복적으로 수행되면 정확한 Vπ로의 수렴은 limit안에서만 발생한다.
그렇다면 우리는 수렴할 때까지 big computation을 기다리거나 그 전에 종료시켜야 할까?
gird world example에서 3번 이상의 policy iteration이 greedy policy improve에 큰 영향을 주지 않는다는 특성은 policy evaluation을 줄일 수 있다는 것을 의미한다.
실제로, policy evaluation step은 policy iteration의 수렴 보장을 잃지 않고 여러가지 방법으로 자를 수 있다.
단 한가지 특별한 case는 단 한번의 sweep 후에 policy evaluation이 중지되는 경우이다. (one backup of each state)
Value Iteration: policy improvement + truncated policy evaluation된 simple backup operation

- Bellman optimality equation으로 표현이 가능하다.
Bellman optimality equation을 update rule로 바꾼 것이다.
- policy evaluation처럼 value iteration은 V*에 정확히 수렴하기 위해서 infinite iteration이 필요하다.
실제로 우리는 sweep에서 value function이 약간만 변경되면 멈춘다.
- 각 sweep에서 하나의 policy improvement sweep과 하나의 policy evaluation sweep을 효율적으로 결합했다.
더 빠른 수렴은 종종 각 policy improvement sweep 사이에 여러 policy evaluation sweep을 삽입하여 달성된다.
일반적으로, truncated policy iteration algorithms의 전체 클래스는 sweep sequence로 생각할 수 있으며, 일부는 policy evaluation backups를 사용하고 일부는 value iteration backups를 사용한다.
max operation이 두가지 backups 간의 유일한 차이이므로 이는 max operation이 policy evaluation의 일부 sweep에 추가된다는 것을 의미한다. 이러한 모든 algorithms는 discounted finite MDP에 대한 optimal policy로 수렴된다.

115
'논문 리뷰 > RL' 카테고리의 다른 글
| code (0) | 2021.07.26 |
|---|---|
| DRQN1 (0) | 2021.05.12 |
| DRQN (0) | 2021.03.25 |
| 03. Finite Markov Decision Process (0) | 2021.03.20 |
| Vanila Actor-Critic (0) | 2021.03.09 |
| REINFORCE(MC-PG) + vanila Policy Gradient (0) | 2021.03.04 |



댓글