Abstract
Introduction
Background
Abstract
MORL(Multi-Objective RL)이란?
: 현실 세계의 문제들은 multiple, possibly conflicting objective들의 optimization을 포함한다. MORL은 scalar reward signal가 각 objective에 대해 하나씩, multiple feedback signals로 확장되는 generalization of standard RL generalization이다. MORL는 multiple criteria를 simultaneously optimize하는 learning policy의 진행 방식이다.
Pareto Q-learning 요약
: 해당 논문에서는 Pareto Q-learning이라는 Pareto dominance relation을 통합한 새로운 TD learning algorithm을 제공한다. 이 algorithm은 single-run안에 set of Pareto dominating policies를 학습하는 multi-policy algorithm이다. 이는 episodic environments에서 stochastic transition function뿐만 아니라 determinisitc에도 적용이 가능하다.
중요한 측면은 Q-vector set를 bootstrap하는 update mechanism이다. 이 vector에서 contribution 중 하나는 expected future discounted reward vector에서 expected immediate reward vector를 분리하는 mechanism이다. 이 decomposition를 통해 set를 update하고 learned policy를 state-space 전체에서 consistently 활용이 가능하다.
Introduction
많은 현실 세계의 문제들은 multiple objective에 의해 작용한다. 예를 들어, wireless sensor network는 energy consumption과 latency라는 conflicting objectives를 가진다. 만약 engineer가 한 개 이상의 objective를 optimize하고 싶다해도, 어떤 objective가 correlated and influence each other 하는지 항상 명확하지 않다. 따라 objective과 conflicting하기 때문에 일반적으로 single optimal solution이 없다. 이러한 경우 objective balance를 유지하는 set of trade-off solution이 필요하다. 정확하게는 set of best trade-off solutions를 얻는, 즉 Pareto가 다른 모든 solution을 지배하지만 mutually incomparable한 solution을 얻고자 한다.
multiple-objective problems dealing approaches
scalarization function
: multi-objective problem을 standard single-objective problem으로 변환하는 방식이다. 그러나 이러한 변환은 scalarization function이 non-linear한 경우 valid 하지 않다. 각 execution이 single solution으로 converge하기 때문에 single-policy algorithm이라고도 부른다. 다양한 trade-off solutions를 찾기 위해 여러 parameterized scalarization function를 사용하고 그 결과를 결합한다. 그러나 weight space에서 objective space로의 mapping이 isomophic을 보장하지는 않는다. 이는 Pareto front of Policies를 잘 적용하기 위해 weight를 정의하는 방법이 명확하지 않다는 뜻이기도 하다.
multi-policy algorithm
: 한 번에 single solution에만 집중하는 것과 다르게, single run에서 set of optimal solution을 검색한다. 이러한 evolutionary multi-objective algorithms는 multi-objective optimization problem를 해결하기 위한 강력한 기술 중 하나이다. 해당 논문에서는 이 방식을 채택한다.
Pareto Q-learning은 convex hull에 국한되지 않고, 충분한 exploration이 제공되면 Deterministic non-stationary policy의 entire Pareto front를 학습할 수 있다. single-objective algorithm 위에 scalarization layer만 추가하는 single-policy approach와 다르게 learning algorithm의 핵심 원칙을 확장하여 set of non-dominated policies를 학습한다. PQL algorithm은 특히 적절한 action을 선택하는 sampling cost가 중요하고 시간이 지남에 따라 성능이 점진적으로 증가해야하는 online use에 적합하다.
학습 중 exploration과 exploitation을 맞추기 위해 online action selection strategies의 기초를 제공하는 sets에 대한 세 가지 evaluation mechanism을 제안한다. 이는 e-greedy와 같은 standard action selection strategies를 수용하기 위해 vector set를 evaluation한다. 이러한 evaluation mechanism은 sets의 내용을 기반으로 learning process 전반에 걸쳐 가능한 최상의 action을 선택하기 위해 hyper volume metric, cardinality indicator, Pareto dominance와 같은 다 객관적 지표를 사용한다.
Background
Reinforcement Learning
* pi: deterministic stationary policy
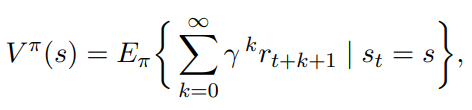

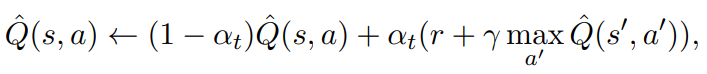

Multi-Objective Reinforcement Learning

multi-objective optimization에서 objective space는 두 개 이상의 dimensions로 구성된다. 따라서 regular MDP는 multi-objective MDP 또는 MOMDP로 generalized 된다. MOMDP는 scalar reward 대신 vector reward를 제공하는 MDP이다. 여기서 m은 objective 개수를 나타낸다. MORL의 경우, state s에서의 state-value function은 vector이다.

env가 multiple objectives를 포함하게 되면서, different policies는 optimal different objectives가 될 수 있다. MORL에는 different optimality criteria가 사용된다. 일반적으로 Pareto dominance relation은 multi-objective optimization에서 optimality criterion으로 사용된다.
Single-Policy MORL

* w: weight vector parameterizing f
: scalarization function을 사용하여 vector-valued policy에 대한 utility를 정의하고 기본 multi-objective env를 single scalar dimention으로 축소시킨다.
general framework에서는 scalar Q^-values는 각 objective에 대한 Q^-values를 저장하는 Q^-vector로 확장된다. 즉, env의 특정 state에서 action을 선택할 때, scalarization function f가 single scalar SQ^(s,a) estimate를 얻기 위해 각 작업을 수행한다.
SQ^(s,a) estimate를 list에 저장하여 예를 들어 e-greedy strategy와 같은 전통적인 action selection strategies를 적용한다.

Scalarized Multi-Objective Q-learning
1: state, action, objective의 각 삼중항에 대한 Q^-values가 초기화된다.
3: agent는 state s에서 각 episode를 시작한다.
5: multi-objective action selection strategy에 따라 action을 select한다.
6: action a를 취하면, env는 agent를 next_state s'으로 전환하고 sampled reward vector r를 제공한다.
8: Q-table이 각 objective에 대해 separate value를 통합하도록 확장됨에 따라 이러한 values는 각 objective에 대해 개별적으로 update된다.
9: single objective Q-learning update 규칙은 multi-objective env에 대해 확장된다.
보다 정확하게는 state s, action a, objective o의 각 삼중항에 대한 Q-value는 각objective r에 대한 해당 reward를 사용하여 next_state s'의 best scalarized action 방향으로 update된다.
이 framework는 standard RL의 action selection mechanism 위에 scalarization layer만 추가한다는 점에 유의해야 한다.


scalarization function은 다양한 형태로 존재할 수 있지만 일반적으로는 linear scalarization function을 사용한다. Q^-vector와 음이 아닌 weight vector의 weighted-sum을 계산한다. weight vector는 다음의 수식을 만족해야만 한다.


이러한 SQ^-value가 주어지면 standard action selection strategies는 선택할 적절한 action을 결정할 수 있다. 예를 들어 greedy case의 경우 가장 큰 SQ^-value를 가진 action이 선택된다. 이 때, linear scalarization function은 convex combination을 계산하기 때문에 Pareto front의 convex region에만 있는 policy를 찾을 수있다는 근본적 한계가 존재한다.

대체 scalar function은 L_p metric을 기반으로 한다. 이 metric은 multi-objective space의 point x아 utopian point z* 사이의 거리를 측정한다. utopian point z*는 각 objective o에 대해 지금까지 최상의 값을 기록함으로써 학습 과정에서 지속적으로 조정되는 parameter이며, 문제가 최소화 되어야하는지 혹은 최대화 되어야하는지에 다라 small negarive or poisitve constatnt T를 더한다. 우리의 설정에서 1≤p≤∞로 x에서 z*까지의 각 objective 사이의 거리를 측정한다.
p=∞인 경우, metric은 weighted L_∞ 또는 Chebyshev metric이 된다.

single-policy MORL인 경우, state-action pair (s,a)의 Q^-vector에 x를 대입하여 SQ^_L∞-value를 얻는다.

L_p metric은 minimal SQ^_L∞-value에 해당하는 action이 state s에서 greedy action으로 고려된다. 따라서 greedy_L∞(s) Chebyshev metric의 경우 다음과 같다.

Chebyshev metric은 일반적이고 확립된 function이지만 이론적 보장이 부족하다. 더 정확하게는 non-linear function인 Chebyshev metric이 scalarized returns가 additive라는 것을 보장하지 않는다는 것을 나타내는 예가 존재한다. 그럼에도 불구하고 이론적 보장이 없다고해도 scalarized MORL algorithm은 고품질 solution을 얻을 수 있다.
Quality indicator
: vector set에 real value를 할당하는 function이며 일반적으로 multi-objective algorithms의 결과를 평가하는데 사용된다. 그러나 특정 multi-objective algorithm은 internal working에서 indicator를 사용하여 search process를 조정하기도 한다. 이 algorithm class를 indicatorbased algorithm이라고 한다.

많은 quality indicator가 존재하지만, hypervolume measure는 elements 및 reference point에 대한 volume을 계산하여 특정 vector solution set를 평가하는 quality indicator이다. 목표는 hypervolume을 최대화하는 것이므로 이 reference point는 일반적으로 env에서 각 목표의 lower limit을 결정하여 정의된다.
Hypervolume indicator
: Pareto dominance와 관련하여 strictly increasing하는 것으로 알려진 유일한 quality measure이므로 multi-object optimization에서 특히 중요하다.
Multi-policy MORL
White(1982)'s DP algorithm
single-policy MORL과 다르게 multi-policy algorithms은 objective space의 차원을 줄이지 않고 한 번에 optimal solution을 학습하는 것을 목표로 한다.

* R(s,a): state s에서 action a를 취한 후 observed expected reward vector
* T(s'|s,a): (s,a)에서 state s'에 도달하는 transition probability
set of Pareto dominating policies를 계산하는 DP algorithm이다. DP는 env model을 가정하는 반면 RL은 env에 대한 사전 지식이 필요하지 않지만 model 없이 작업할 수 있다는 점이 다르다.
우리는 V^ND(s')을 s'에서의 각 action에 대한 ^Q_set의 non-dominated vector로 참조한다.

아래의 operator +는 input set의 모든 Pareto dominated elements를 제거하고 non-dominated elements set를 반환하는 function이다.

아이디어는 discounted Pareto dominating reward가 propagate되고, Q^set이 set of Pareto dominating policies로 수렴된 후 사용자가 preference function을 적용하여 Q^set tree를 탐색할 수 있다는 것이다. MORL의 경우, determinisitc non-stationary policy, 즉 current state 뿐만 아니라 time-step t에도 적용되는 policy이 Pareto가 최고의 deterministic stationary policy를 dominate할 수 있음을 보여주었다.
결과적으로 disount factor에 대한 값이 큰 infinite horizon 문제에서 non-stationary policy의 수가 exponentially하게 증가하므로 set의 폭발로 이어질 수 있다.
Barrett & Narayanan's CHVI algorithm

: Pareto front의 convex hull에 있는 deterministic stationary policy를 계산하는 convex hull value-iteration을 제안했다. convex hull은 policy pi, V_pi, weight vector w의 linear combination이 maximal인 policy set이다. 그림(a)에서 흰색 점은 bi-objective 문제의 Pareto front를 나타내고, 그림(b)의 빨간색 선은 해당 convex hull을 나타낸다. 빨간 점으로 표시된 deterministic policies는 CHVI가 학습할 policies다. CHVI는 s'의 모든 action, 즉 Q(s',a')에 대한 합집합의 convex hull을 계산하여 bootstrap한다.
결론적으로 (1) 방법은 env model이 알려져 있다고 가정하는 batch algorithm이라는 것을 염두하고, (2) 방법은 Pareto front의 subset, 즉 convex hull에 있는 policy만 얻는다.
Vamplew's mixture policy
: 앞서 언급한 multi-policy algorithms는 deterministic policies set만 학습하지만 이러한 policies의 probabilistic combination을 사용하는 것도 가능하고, 이러한 두 policies의 stochastic combination을 mixture policy라고 부른다.
예를 들어 매우 쉬운 multi-obejctive 문제 agent는 V^pi1(s_0)=(1,0)과 V^pi2(s_0)만 따를 수 있다. 확률이 p인 policy pi1과 확률이 1-p인 policy pi2를 따를 경우 average reward vector는 (p,1-p)가 된다. 따라서 두 가지 deterministic policies가 존재함에도 불구하고, 원래 문제인 mixture policy는 특정 probability와 결합하여 policy의 entire convex hull을 sampling이 가능하다. 따라서 그림(a)의 Pareto front policy의 stochastic combinations는 그림(b)의 빨간색 선의 모든 solution을 나타낼 수 있다. 그러나 mixture policy는 모든 상황에서 적절하지 않을 수 있다.
Pareto Q-learning
https://www.jmlr.org/papers/volume15/vanmoffaert14a/vanmoffaert14a.pdf
'개인 정리 > 개념 정리' 카테고리의 다른 글
| Attention Is All You Need (0) | 2022.03.11 |
|---|---|
| Deep RL Policy-based Method (0) | 2022.03.04 |
| Deep RL Value-based Methods (0) | 2022.03.03 |
| Traditional RL (0) | 2022.03.02 |
| Combinatorial Optimization by POMO (0) | 2022.03.01 |
| Model-free RL, Model-based RL (0) | 2022.02.07 |




댓글